题目内容
14. 如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.
如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.
分析 AM=CN,首先根据AC=BD可得AB=CD,由AM∥CN,BM∥DN,得到∠A=∠NCD,∠MBA=∠D,证明△AMB≌△CND,即可解答.
解答 解:AM=CN,
理由:∵AC=BD,
∴AC+CB=DB+CB,
即:AB=CD,
∵AM∥CN,BM∥DN,
∴∠A=∠NCD,∠MBA=∠D,
在△AMB和△CND中,
$\left\{\begin{array}{l}{∠A=∠NCD}\\{AB=CD}\\{∠MBA=∠D}\end{array}\right.$
∴△AMB≌△CND(ASA),
∴AM=CN.
点评 此题主要考查了三角形全等的判定方法和性质,以及平行线的判定,关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
| A. | 6,$3\sqrt{2}$ | B. | $3\sqrt{2}$,3 | C. | 6,3 | D. | $6\sqrt{2}$,$3\sqrt{2}$ |
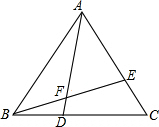 如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F
如图,已知在等边△ABC中,点D、E分别在BC,AC上,BD=CE,AD与BE交于点F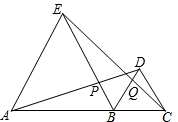 如图,△BDE与△BCD均为等边三角形,连接AD交BE于P,连接CE交BD于Q.
如图,△BDE与△BCD均为等边三角形,连接AD交BE于P,连接CE交BD于Q. 如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.
如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.