题目内容
12. 如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由.
分析 (1)由正方形的性质得出∠ABE=∠BCF=90°,AB=BC,由SAS证明△ABE≌△BCF,得出对应边相等即可;
(2)由全等三角形的性质得出∠BAE=∠CBF,由角的互余关系证出∠BGE=90°,即可得出结论.
解答 解:(1)AE=BF;理由如下:
∵四边形ABCD是正方形,
∴∠ABE=∠BCF=90°,AB=BC,
在△ABE和△BCF中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABE=∠BCF}&{\;}\\{BE=CF}&{\;}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)AE⊥BF;理由如下:
由(1)得:△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BGE=90°,
∴AE⊥BF.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
3.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
| A. | 6,$3\sqrt{2}$ | B. | $3\sqrt{2}$,3 | C. | 6,3 | D. | $6\sqrt{2}$,$3\sqrt{2}$ |
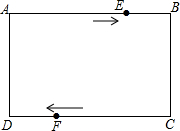 如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t.
如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t. 如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.
如图,$\widehat{AB}$的度数为90°,点C、D将$\widehat{AB}$三等分,弦AB与半径OC、OD交于点E、F,求证:AE=CD=FB.