题目内容
如图，已知：AB=AD，∠BAC=∠DAC，若过A点作AE⊥BC于E，AF⊥CD于F，求证：AE=AF．考点：全等三角形的判定与性质,角平分线的性质
专题：证明题
分析：首先证明△BAC≌△DAC，所以∠ECA=∠FCA，在根据条件AE⊥BC于E，AF⊥CD于F，即可证明AE=AF．
解答：证明：在△BAC和△DAC中，
，
∴△BAC≌△DAC（SAS），
∴∠ECA=∠FCA，
∵AE⊥BC于E，AF⊥CD于F，
∴AE=AF．
|
∴△BAC≌△DAC（SAS），
∴∠ECA=∠FCA，
∵AE⊥BC于E，AF⊥CD于F，
∴AE=AF．
点评：本题考查了全等三角形的和性质以及角平分线的性质定理：角的平分线上的点到角的两边的距离相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
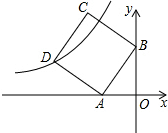如图，在平面直角坐标系中，直线y=2x+4与x轴、y轴分别交于A、B两点，以AB为边在第二象限作正方形ABCD，点D在双曲线y=
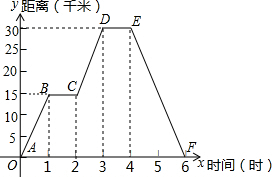小明同学骑自行车去郊外春游，如图为表示他离家的距离y（千米）与所用的时间x（时）之间关系的函数图象．
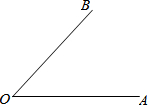已知∠AOB（如图），求作：