题目内容
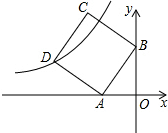 如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=
如图,在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线y=| k |
| x |
| A、1 | B、2 | C、3 | D、4 |
考点:反比例函数综合题
专题:
分析:作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F,易证△OAB≌△FDA≌△BEC,求得A、B的坐标,根据全等三角形的性质可以求得C、D的坐标,从而利用待定系数法求得反比例函数的解析式,进而求得G的坐标,则a的值即可求解.
解答:解:过点CE⊥y轴于点E,交双曲线于点G,过点D作DF⊥x轴于点F,
在y=2x+4中,令x=0,解得:y=4,即B的坐标是(0,4),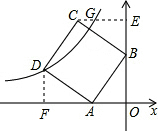
令y=0得:x=-2,即A的坐标是(-2,0),
则OB=4,OA=2,
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
,
∴△OAB≌△FDA,
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=4,DF=OA=BE=2,
∴D的坐标是(-6,2),C的坐标是(-4,6).
将点D代入y=
得:k=-12,
则函数的解析式是:y=-
∴OE=6,
则C的纵坐标是6,把y=6代入y=-
得:x=-2,
则G的坐标是(-2,6),
∴CG=4-2=2.
∴a=2.
故答案为:2.
在y=2x+4中,令x=0,解得:y=4,即B的坐标是(0,4),

令y=0得:x=-2,即A的坐标是(-2,0),
则OB=4,OA=2,
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
|
∴△OAB≌△FDA,
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=4,DF=OA=BE=2,
∴D的坐标是(-6,2),C的坐标是(-4,6).
将点D代入y=
| k |
| x |
则函数的解析式是:y=-
| 12 |
| x |
则C的纵坐标是6,把y=6代入y=-
| 12 |
| x |
则G的坐标是(-2,6),
∴CG=4-2=2.
∴a=2.
故答案为:2.
点评:本题考查了反比例函数综合,用到的知识点是正方形的性质、全等三角形的判定与性质以及待定系数法求函数的解析式等,难度适中,正确求得C、D的坐标是关键,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
x<y,那么化简y-x-
为( )
| (x-y)2 |
| A、0 | B、2y |
| C、-2x | D、2y-2x |
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、(
| ||||||||
D、
|
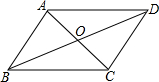 如图,平行四边形ABCD的对角线相交于点O,AB=6cm,两条对角线长度之和为24cm,则△COD的周长为( )cm.
如图,平行四边形ABCD的对角线相交于点O,AB=6cm,两条对角线长度之和为24cm,则△COD的周长为( )cm.| A、24 | B、21 | C、15 | D、18 |
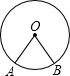 如图,A、B是⊙O上两点,且∠AOB=70°,点C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是( )
如图,A、B是⊙O上两点,且∠AOB=70°,点C是⊙O上不与点A、B重合的任一点,则∠ACB的度数是( )| A、35° |
| B、145° |
| C、35°或145° |
| D、35°或110° |
 如图,线段AC是矩形ABCD的对角线,
如图,线段AC是矩形ABCD的对角线, 如图,已知:AB=AD,∠BAC=∠DAC,若过A点作AE⊥BC于E,AF⊥CD于F,求证:AE=AF.
如图,已知:AB=AD,∠BAC=∠DAC,若过A点作AE⊥BC于E,AF⊥CD于F,求证:AE=AF.