题目内容
9.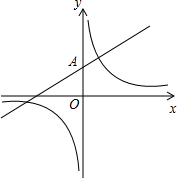 已知直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{m}{x}$的一个交点为(2,5),直线与y轴交于点A.
已知直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{m}{x}$的一个交点为(2,5),直线与y轴交于点A.(1)求m的值及点A的坐标;
(2)若点P在双曲线y=$\frac{m}{x}$的图象上,且S△POA=10,求点P的坐标.
分析 (1)利用待定系数法即可求得反比例函数和一次函数的解析式,然后求得A的坐标;
(2)设P的横坐标是m,根据三角形的面积公式求得P的横坐标,进而求得P的坐标.
解答 解:(1)把(2,5)代入y=$\frac{m}{x}$得m=10;
把(2,5)代入y=$\frac{1}{2}$x+b得1+b=5,解得b=4,
则直线的解析式是y=$\frac{1}{2}$x+4,
令x=0,解得y=4,
则A的坐标是(0,4);
(2)设P的横坐标是m,
则$\frac{1}{2}$×4|m|=10,
解得m=±5.
当x=m=5时,代入y=$\frac{10}{x}$得y=2,则P的坐标是(5,2),
当x=-5时,代入y=$\frac{10}{x}$得y=-2,则P的坐标是(-5,-2).
则P的坐标是(5,2)或(-5,-2).
点评 本题考查了待定系数法求函数解析式,以及反比例函数与一次函数的交点,注意到P应该分成两种情况是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.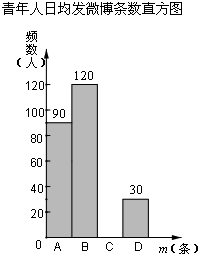 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:
18-35岁青年人日均发微博条数统计表
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.
 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:18-35岁青年人日均发微博条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(m≥15) | 30 | 0.1 |
(1)求a,b;
(2)补全频数分布直方图.
4. 如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.
 如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.
| A. | ①②③ | B. | ②③ | C. | ①② | D. | ①③ |
18. 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )| A. | 14 cm | B. | 18 cm | C. | 24 cm | D. | 28 cm |
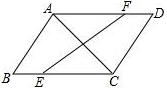 已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.
已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.