题目内容
2.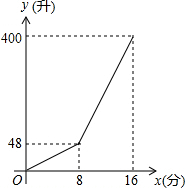 一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.(1)分别求出A、B两注水管的注水速度.
(2)当8≤x≤16时,求y与x之间的函数关系式.
(3)当两水管的注水量相同时,直接写出x的值.
分析 (1)根据注水总量=注水速度×注水时间,即可分别求出A、B两注水管的注水速度;
(2)当8≤x≤16时,设y与x的函数关系为y=kx+b,根据点(8,48)、(16,400)的坐标利用待定系数法,即可求出y与x之间的函数关系式;
(3)由注水总量=注水速度×注水时间,即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)A注水管注水速度为45÷8=6(升/分),
B注水管注水速度为(400-6×16)÷(16-8)=38(升/分).
答:A注水管的注水速度为6升/分,B注水管的注水速度为38升/分.
(2)当8≤x≤16时,设y与x的函数关系为y=kx+b,
将(8,48)、(16,400)代入y=kx+b,
$\left\{\begin{array}{l}{8k+b=48}\\{16k+b=400}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=44}\\{b=-304}\end{array}\right.$.
∴当8≤x≤16时,y与x之间的函数关系式为y=44x-304.
(3)根据题意得:6x=38(x-8),
解得:x=9.5.
答:当两水箱注水量相同时,x的值为9.5.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及解一元一次方程,解题的关键是:(1)根据注水总量=注水速度×注水时间,列式计算;(2)根据点的坐标,利用待定系数法求出函数关系式;(3)根据注水总量=注水速度×注水时间,列出关于x的一元一次方程.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.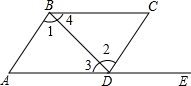 如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )
如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )
 如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )
如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠CDE | D. | ∠C+∠1+∠4=180° |
10.若(x3)m=x9,则m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.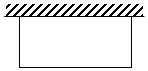 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.
(1)当垂直于墙的一边比另一边少7米时,求长方形的面积.
(2)按表中列出的数据要求,填写表格.
观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.(1)当垂直于墙的一边比另一边少7米时,求长方形的面积.
(2)按表中列出的数据要求,填写表格.
观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
| 垂直于墙的一边比另一边少(m) | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
11.将点A(-1,2)向右平移4个单位长度,再向下平移3个单位长度,则平移后点的坐标是( )
| A. | (3,1) | B. | (-3,-1) | C. | (3,-1) | D. | (-3,1) |
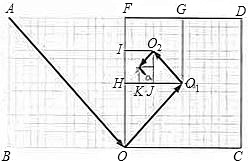 如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走2走到正方形O3KJP的中心O4,一共走了31$\sqrt{2}$m,则长方形花坛ABCD的周长是96m.
如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走2走到正方形O3KJP的中心O4,一共走了31$\sqrt{2}$m,则长方形花坛ABCD的周长是96m.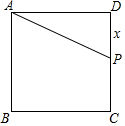 如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.