题目内容
9.已知:x=$\frac{1}{2}$-$\frac{\sqrt{5}}{2}$,y=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$,计算:(1)-3x2+12xy-3y2.
(2)-7x2-32xy-7y2.
分析 (1)将原式利用完全平方公式变形进而利用已知代入求出即可;
(2)将原式利用完全平方公式变形进而利用已知代入求出即可.
解答 解:(1)-3x2+12xy-3y2
=-3(x2-2xy+y2-2xy)
=-3(x-y)2+6xy,
将x=$\frac{1}{2}$-$\frac{\sqrt{5}}{2}$,y=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$代入得出:
原式=-3($\frac{1}{2}$-$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$-$\frac{\sqrt{5}}{2}$)2+6($\frac{1}{2}$-$\frac{\sqrt{5}}{2}$)($\frac{1}{2}$+$\frac{\sqrt{5}}{2}$)
=-15-6
=-21;
(2)-7x2-32xy-7y2
=-7(x2+2xy+y2)-18xy
=-7(x+y)2-18xy
将x=$\frac{1}{2}$-$\frac{\sqrt{5}}{2}$,y=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$代入得出:
原式=-7-18($\frac{1}{2}$-$\frac{\sqrt{5}}{2}$)($\frac{1}{2}$+$\frac{\sqrt{5}}{2}$)=11.
点评 此题主要考查了二次根式的化简求值,正确利用完全平方公式是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
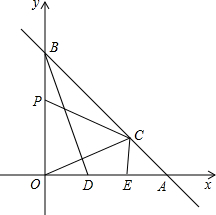 如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0
如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0