题目内容
1.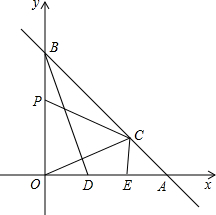 如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0
如图,直线L交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0(1)求A、B两点坐标;
(2)C为线段AB上一点,C点的横坐标是3,P是y轴正半轴上一点,且满足∠OCP=45°,求P点坐标;
(3)在(2)的条件下,过B作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
分析 (1)由(a-b)2+|b-4|=0,利用非负数的性质得到a-b=0,b-4=0,解得a=4,b=4,得到A(4,0),B(0,4);
(2)如图1过点O作OM⊥OC交CP的延长线于M,得到等腰直角三角形,根据其性质得到OM=OC,利用直线AB的解析式,求出点C的坐标,从而得到点M的坐标,求得直线CM 的解析式,得到P点的坐标;
(3)过点A作AF⊥x轴,交OC的延长线于F,证明△BOD与△OAF,△ACE与△ACF全等,得到AE=AF,OD=AF,由等量代换得到OD=AE.
解答 (1)解:∵(a-b)2+|b-4|=0,
∴a-b=0,b-4=0,
∴a=4,b=4,
∴A(4,0),B(0,4);
(2)如图1过点O作OM⊥OC交CP的延长线于M,
∵∠OCP=45°,
∴△OMC是等腰直角三角形,
∴OM=OC,
设直线AB的解析式为:y=kx+4,
∴0=4k+4,
∴k=-1,
∴直线AB的解析式为:y=-x+4,
当x=3时,y=1,
∴C(3,1),
∴M(-1,3),
∴直线CP的解析式为:y=-$\frac{1}{2}$x+$\frac{5}{2}$,
∴P(0,$\frac{5}{2}$);
(3)过点A作AF⊥x轴,交OC的延长线于F,由(1)证得OA=OB,由(2)的条件得∠DBO=∠AOF,
∵∠BOD=∠OAF=90°,
在△BOD与△OAF中,$\left\{\begin{array}{l}{∠DBO=∠AOF}\\{OA=OB}\\{∠BOD=∠OAF}\end{array}\right.$,
∴△BOD≌△OAF,
∴OD=AF,∠BDO=∠AFO,
∵∠CAE=∠CAF=45°,
∵∠CEA=∠BDO,
∴∠CEA=∠AFO,
在△ACE与△ACF中$\left\{\begin{array}{l}{∠CEA=∠AFO}\\{AC=AC}\\{∠CAE=∠CAF}\end{array}\right.$,
∴△ACE≌△ACF,
∴AE=AF,
∵OD=AF,
∴OD=AE.
点评 本题考查了非负数的性质,求点的坐标,待定系数法求函数的解析式,全等三角形的判定与性质,解题的关键是正确的作出辅助线.

 今年8月,我省大部分地区出现强降雨天气,洪水时刻威胁着人民的生命财产安全.下面是小明对某一水库的观测记录,他取警戒水位为0米,该水库一周内的水位变化情况如下:(测量前一天的水位达到了警戒水位,单位:米)
今年8月,我省大部分地区出现强降雨天气,洪水时刻威胁着人民的生命财产安全.下面是小明对某一水库的观测记录,他取警戒水位为0米,该水库一周内的水位变化情况如下:(测量前一天的水位达到了警戒水位,单位:米)| 时间 | 8月5日 | 8月6日 | 8月7日 | 8月8日 | 8月9日 | 8月10日 | 8月11日 |
| 水位变化/米 | +0.15 | -0.2 | +0.13 | -0.1 | +0.14 | -0.25 | +0.16 |
(1)这周内,哪一天的水位最高,哪一天的水位最低?它们是位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与测量前一天比,一周内水库的水位是上升了,还是下降了?
(3)以警戒水位为0点,用折线统计图表示这一周水位的变化情况.(在坐标纸里画图)
| n | 16 | 0.16 | 0.0016 | 1600 | 16000 | … |
| $\sqrt{n}$ | 4 | 0.4 | 0.04 | 40 | 400 | … |
(2)运用你发现的规律,探究下列问题:已知$\sqrt{2.06}$≈1.435,求下列各数的算术平方根:
①0.0206≈0.1435; ②20600≈143.5;
(3)根据上述探究过程类比研究一个数的立方根已知$\root{3}{2}$≈1.260,则$\root{3}{2000}$≈12.60.