题目内容
3.已知:有理数m所表示的点到点1距离2个单位长度,a,b互为相反数,且均不为零,c,d互为倒数.求:$\frac{3a+3b}{m}$-2cd+m2的值.分析 根据绝对值、数轴、相反数、倒数求出m=3或-1,a+b=0,cd=1,再代入求出即可.
解答 解:∵有理数m所表示的点到点1距离2个单位长度,a,b互为相反数,且均不为零,c,d互为倒数,
∴m=3或-1,a+b=0,cd=1,
当m=3时,$\frac{3a+3b}{m}$-2cd+m2
=$\frac{3×0}{3}$-2×1+32
=7;
当m=-1时,$\frac{3a+3b}{m}$-2cd+m2
=$\frac{3×0}{3}$-2×1+(-1)2
=-1.
点评 本题考查了求代数式的值、相反数、倒数、绝对值、数轴等知识点,能求出m=3或-1、a+b=0、cd=1是解此题的关键.

练习册系列答案
相关题目
18.某校的一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.
(1)请你在表的空格里填写一个适当的代数式:
(2)已知第15排座位数是第5排座位数的2倍,求a的值;
(3)在(2)的条件下计算第21排有多少座位?
(1)请你在表的空格里填写一个适当的代数式:
| 第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … | 第n排的 座位数 |
| 12 | 12+a | 12+2a | 12+3a | … | 12+(n-1)a |
(3)在(2)的条件下计算第21排有多少座位?
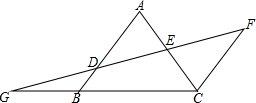 如图,AB∥FC,D是AB上一点,且DE=EF,DF交AC于点E,分别延长FD和CB交于点G
如图,AB∥FC,D是AB上一点,且DE=EF,DF交AC于点E,分别延长FD和CB交于点G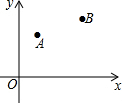 A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图的平面直角坐标系.
A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图的平面直角坐标系. 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上). 如图,∠AOB=90°,∠BOC=2∠BOD,OD平分∠AOC,求∠BOD的度数.
如图,∠AOB=90°,∠BOC=2∠BOD,OD平分∠AOC,求∠BOD的度数.