题目内容
14.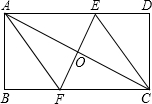 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.(1)连接AF,CE,求证:四边形AFCE为菱形;
(2)求AF的长.
分析 (1)根据矩形的性质得出AD∥BC,求出∠AEO=∠CFO,根据全等三角形的判定得出△AEO≌△CFO,根据全等三角形的性质得出OE=OF,根据菱形的判定推出即可;
(2)设AF=acm,根据菱形的性质得出AF=CF=acm,在Rt△ABF中,由勾股定理得出42+(8-a)2=a2,求出a即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEO=∠CFO,
∵AC的垂直平分线EF,
∴AO=OC,AC⊥EF,
在△AEO和△CFO中
∵$\left\{\begin{array}{l}∠AEO=∠CFO\\∠AOE=∠COF\\ AO=OC\end{array}\right.$
∴△AEO≌△CFO(AAS),
∴OE=OF,
∵O A=OC,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴平行四边形AECF是菱形;
(2)解:设AF=acm,
∵四边形AECF是菱形,
∴AF=CF=acm,
∵BC=8cm,
∴BF=(8-a)cm,
在Rt△ABF中,由勾股定理得:42+(8-a)2=a2,
解得:a=5,
即AF=5cm.
点评 本题考查了菱形的性质和判定,全等三角形的性质和判定,线段垂直平分线的性质,勾股定理的应用,能综合运用定理进行推理是解此题的关键,注意:对角线互相垂直的平行四边形是菱形.

练习册系列答案
相关题目
5.下列各式,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{2}-\sqrt{2}$=3 | C. | 2$\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | D. | ($\sqrt{8}-\sqrt{6}$)$÷\sqrt{2}=2-\sqrt{3}$ |
 如图,要使平行四边形ABCD成为矩形,应添加的条件是AC=BD(只需填一个你认为正确的结论即可).
如图,要使平行四边形ABCD成为矩形,应添加的条件是AC=BD(只需填一个你认为正确的结论即可).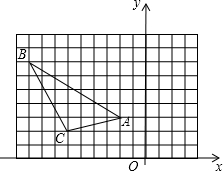 如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.
如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.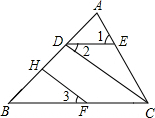 填空并完成以下证明:
填空并完成以下证明: 如图,已知△ABC为等腰三角形,AB=AC,延长CB和BC至点D、点E,使得BD=CE,试说明AD=AE.
如图,已知△ABC为等腰三角形,AB=AC,延长CB和BC至点D、点E,使得BD=CE,试说明AD=AE. 如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.
如图,将长方形ABCD沿折痕EF对折,使点C与点A重合,若∠AEB=50°,则∠AFE=65°.