题目内容
1.商店出售下列形状的地砖:①长方形;②正方形;③正五边形;④正六边形.
若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
解答 解:①长方形的每个内角是90°,4个能组成镶嵌;
②正方形的每个内角是90°,4个能组成镶嵌;
③正五边形每个内角是180°-360°÷5=108°,不能整除360°,不能镶嵌;
④正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖有①②④.
故选C.
点评 此题主要考查了平面镶嵌,用一种正多边形的镶嵌应符合一个内角度数能整除360°.任意多边形能进行镶嵌,说明它的内角和应能整除360°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地抽查了n人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这n人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=22}\\{x×2.5%+y×0.5%=n}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=22}\\{\frac{x}{2.5%}+\frac{y}{0.5%}=n}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=22}\\{x×2.5%-y×0.5%=22}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=22}\\{\frac{x}{2.5%}-\frac{y}{0.5%}=22}\end{array}\right.$ |
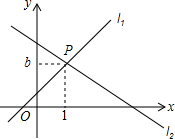 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b). 填空并完成以下证明:
填空并完成以下证明: