题目内容
2.若扇形的圆心角为60°,面积为$\frac{2}{3}$π,则这个扇形的半径为2,弧长为$\frac{2}{3}$π.分析 首先根据扇形的面积公式求出扇形的半径,再根据扇形的面积=$\frac{1}{2}$lR,即可得出弧长.
解答 解:设扇形的半径为r,弧长为l,
根据扇形面积公式得;$\frac{60×π×{R}^{2}}{360}$=$\frac{2}{3}$π,
解得:R=2,
即这个扇形的半径为2;
∵扇形的面积=$\frac{1}{2}$lR=$\frac{2}{3}$π,
解得:l=$\frac{2}{3}$π.
故答案为:2,$\frac{2}{3}$π.
点评 本题考查了扇形面积的计算方法、弧长的计算方法;灵活运用扇形面积的计算方法,求出扇形半径是解决问题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
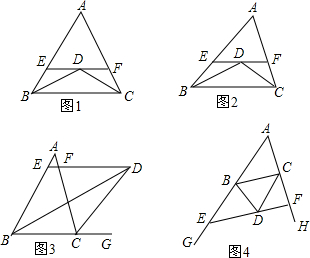
 如图,∠EAB是△ABC的外角,BD平分∠ABC.求证:∠BDE=$\frac{1}{2}$(∠C+∠BAE)
如图,∠EAB是△ABC的外角,BD平分∠ABC.求证:∠BDE=$\frac{1}{2}$(∠C+∠BAE)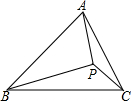 如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.
如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.