题目内容
3.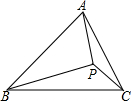 如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.
如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.
分析 延长CP、AP分别交AB、BC于点D、E,连接DE,利用∠PAB=∠PCB和三角形的内角和定理得出∠ADC=∠CAE,证得A、D、E、C四点共圆,得出∠EAC=∠EDC,结合∠PBC=∠PAC,证得B、E、P、D四点共圆,得出∠ADC=∠BDP=∠BEP=∠PEC=90°,证得结论成立.
解答 证明:如图,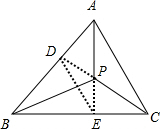
延长CP、AP分别交AB、BC于点D、E,连接DE,
∵∠PAB=∠PCB,∠APD=∠CPE,
∴∠ADC=∠AEC,
∴A、D、E、C四点共圆,
∴∠EAC=∠EDC,
又∵∠PBC=∠PAC,
∴∠PBE=∠EDP,
∴B、E、P、D四点共圆,四边形BEPD是圆内接四边形,
∴∠BDP=∠BEP=∠PEC,
∴∠ADC=∠BDP=∠BEP=∠PEC=90°,
∴CD⊥AB,AE⊥BC,
∴P为△ABC的垂心.
点评 此题考查三角形的垂心,利用垂心的定义,构造出四点共圆的条件,利用圆周角定理、平角的意义证得结论成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知$\sqrt{a+2}+|{b-1}|=0$,那么(a+b)2015的值为( )
| A. | -1 | B. | 1 | C. | 32015 | D. | -32015 |
 如图,已知AB=DE,AF=CD,BC=EF,∠A=∠D,求证:∠C=∠F.
如图,已知AB=DE,AF=CD,BC=EF,∠A=∠D,求证:∠C=∠F.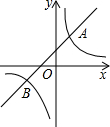 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.