题目内容
4.抛物线y=ax2+bx+1的顶点在第一象限,且过点(-1,0),设t=a+b+1,则t的取值范围是0<t<2.分析 由二次函数的解析式可知,当x=1时,所对应的函数值y=t=a+b+1.把点(-1,0)代入y=ax2+bx+1,a-b+1=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出t=a+b+1的变化范围.
解答 解:∵二次函数y=ax2+bx+1的顶点在第一象限,
且经过点(-1,0),
∴易得:a-b+1=0,a<0,b>0,
由a=b-1<0得到b<1,结合上面b>0,所以0<b<1①,
由b=a+1>0得到a>-1,结合上面a<0,所以-1<a<0②,
∴由①+②得:-1<a+b<1,
在不等式两边同时加1得0<a+b+1<2,
∵a+b+1=t代入得0<t<2,
∴0<t<2.
故答案为:0<t<2.
点评 此题主要考查了二次函数的性质,二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法.同时注意特殊点的运用.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
19.下面四个数中,负数是( )
| A. | 20 | B. | 0 | C. | 3 | D. | -2 |
16.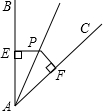 如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
 如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )| A. | HL | B. | ASA | C. | AAS | D. | SAS |
13.已知$\sqrt{a+2}+|{b-1}|=0$,那么(a+b)2015的值为( )
| A. | -1 | B. | 1 | C. | 32015 | D. | -32015 |
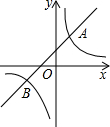 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.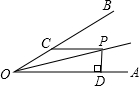 如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.
如图,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD+PC=12,则0C的长为8.