题目内容
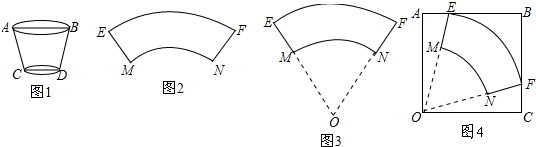
1.某班课题学习小组对无盖的纸杯进行制作与探究,所要制作的纸杯如图1所示,规格要求是:杯口直径AB=6cm,杯底直径CD=4cm,杯壁母线AC=BD=6cm.请你和他们一起解决下列问题:(1)小顾同学先画出了纸杯的侧面展开示意图(如图2,忽略拼接部分),得到图形是圆环的一部分.
①图2中弧EF的长为6πcm,弧MN的长为4πcm;
②要想准确画出纸杯侧面的设计图,需要确定弧MN所在圆的圆心O,如图3所示.小顾同学发现有$\frac{\widehat{EF}的长}{\widehat{MN}的长}$=$\frac{OF}{ON}$,请你帮她证明这一结论.
③根据②中的结论,求弧MN所在圆的半径r及它所对的圆心角的度数n.
(2)小顾同学计划利用正方形纸片一张,按如图甲所示的方式剪出这个纸杯的侧面,求正方形纸片的边长.
分析 (1)①直接根据圆的周长公式计算;
②设它所对的圆心角的度数为n,根据弧长公式得到$\widehat{EF}$的长=$\frac{n•π•OF}{180}$,$\widehat{MN}$的长=$\frac{n•π•ON}{180}$,然后把它们相比即可得到$\frac{\widehat{EF}的长}{\widehat{MN}的长}$=$\frac{OF}{ON}$;
③由(2)中的结论得到得$\frac{OF}{ON}$=$\frac{6π}{4π}$=$\frac{3}{2}$,加上OF=ON+6,可求得ON=12,再利用弧长公式得到$\frac{n•π•12}{180}$=4π,于是可求出n=60°;
(2)如图4,连结EF,OB,它们相交于点P,先证明△OEF为等边三角形得到EF=OF=18,再证明Rt△AOE≌Rt△COF得到AE=CF,则BE=BF,于是可判断OB垂直平分EF,所以PF=$\frac{1}{2}$EF=9,由勾股定理计算出OP=$\sqrt{1{8}^{2}-{9}^{2}}$=9$\sqrt{3}$,由△PFB为等腰直角三角形和得到PB=PF=9,则OB=9$\sqrt{3}$+9,然后根据正方形的性质得OC=$\frac{\sqrt{2}}{2}$OB=$\frac{9\sqrt{6}+9\sqrt{2}}{2}$.
解答 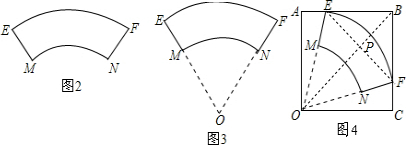 (1)解:①如图2,弧EF的长为6πcm,弧MN的长为4πcm;
(1)解:①如图2,弧EF的长为6πcm,弧MN的长为4πcm;
故答案为6π,4π;
②证明:如图3,设它所对的圆心角的度数为n,
$\widehat{EF}$的长=$\frac{n•π•OF}{180}$,$\widehat{MN}$的长=$\frac{n•π•ON}{180}$,
所以$\frac{\widehat{EF}的长}{\widehat{MN}的长}$=$\frac{OF}{ON}$;
③由(2)得$\frac{OF}{ON}$=$\frac{6π}{4π}$=$\frac{3}{2}$,
而OF=ON+6,
解得ON=12,
即r=12,
因为$\frac{n•π•12}{180}$=4π,
解得n=60°;
(2)解:如图4,连结EF,OB,它们相交于点P,
∵四边形ABCD为正方形,
∴OA=OC,∠OBC=45°,
∵∠OEF=60°,OE=OF,
∴△OEF为等边三角形,
∴EF=OF=18,
在Rt△AOE和Rt△COF中,
$\left\{\begin{array}{l}{OE=OF}\\{OA=OC}\end{array}\right.$,
∴Rt△AOE≌Rt△COF,
∴AE=CF,
∴BE=BF,
∴OB垂直平分EF,
∴PF=$\frac{1}{2}$EF=9,
∴OP=$\sqrt{1{8}^{2}-{9}^{2}}$=9$\sqrt{3}$,
∵△PFB为等腰直角三角形,
∴PB=PF=9,
∴OB=9$\sqrt{3}$+9,
∴OC=$\frac{\sqrt{2}}{2}$OB=$\frac{9\sqrt{6}+9\sqrt{2}}{2}$,
即正方形纸片的边长为$\frac{9\sqrt{6}+9\sqrt{2}}{2}$cm.
点评 本题考查了圆的综合题:熟练掌握圆的有关性质和正方形的性质;记住弧长公式;学会把几何题展开成平面图形的方法解决几何体的问题.

 小题狂做系列答案
小题狂做系列答案| A. | 2x2-7=3y+1 | B. | 5x2+$\frac{1}{x}$+4=0 | C. | $\frac{\sqrt{7}}{3}$x-$\sqrt{5}$=$\frac{{x}^{2}}{2}$+x | D. | ax2+bx+c=0 |
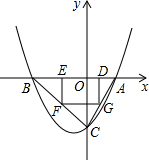 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
 如图,D是等边△ABC内一点,AD=2,BD=1,若将△ABD绕点A旋转后到△ACP位置,则DP的长是2.
如图,D是等边△ABC内一点,AD=2,BD=1,若将△ABD绕点A旋转后到△ACP位置,则DP的长是2.