题目内容
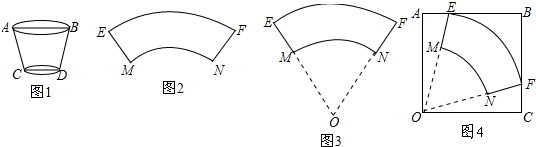
11．
如图，D是等边△ABC内一点，AD=2，BD=1，若将△ABD绕点A旋转后到△ACP位置，则DP的长是2．
分析 根据等边三角形的性质得AB=AC，∠BAC=60°，再根据旋转的性质得AD=AP，∠DAP=∠BAC=60°，则可判断△ADP为等边三角形，然后根据等边三角形的性质求解．
解答 解：∵△ABC为等边三角形，
∴AB=AC，∠BAC=60°，
∵△ABD绕点A旋转后到△ACP位置，
∴AD=AP，∠DAP=∠BAC=60°，
∴△ADP为等边三角形，
∴DP=AD=2．
故答案为2．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．解决本题的关键是判断△ADP为等边三角形．
练习册系列答案
阅读快车系列答案
相关题目
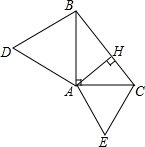△ABC中，∠BAC=90°，分别以AB、AC为边，得到等边△ABD、等边△ACE．过A作AH⊥BC于点H．求证：
如图，在数轴上运用尺规作图法作出点A，则点A表示的数为-$\sqrt{2}$．
3．下列方程是一元二次方程的是（ ）
| A． | ax2+bx+c=0 | B． | x2+2x=x2-1 | C． | $\frac{1}{{x}^{2}}$-x=2 | D． | （x-1）（x-3）=0 |
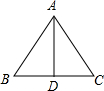如图，在等边△ABC中，AD⊥BC，AB=6，则DC的长为3．