题目内容
(1)解方程:x(x-2)-(x-2)=0
(2)已知:代数式
的值为0,求x的值.
(2)已知:代数式
| x2-2x-3 |
| 2x-6 |
考点:解一元二次方程-因式分解法,分式的值为零的条件
专题:
分析:(1)利用提取公因式(x-2)对等式的左边进行因式分解,然后解方程;
(2)令分子等于零,且分母不等于零,由此可以求得x的值.
(2)令分子等于零,且分母不等于零,由此可以求得x的值.
解答:解:(1)由原方程,得
(x-1)(x-2)=0,
∴x-1=0或x-2=0,
解得 x1=1,x2=2;
(2)∵代数式
的值为0,
∴x2-2x+3=0,且2x-6≠0,
∴(x-3)(x+1)=0,且2(x-3)≠0,
∴x+1=0,
解得x=-1.
(x-1)(x-2)=0,
∴x-1=0或x-2=0,
解得 x1=1,x2=2;
(2)∵代数式
| x2-2x-3 |
| 2x-6 |
∴x2-2x+3=0,且2x-6≠0,
∴(x-3)(x+1)=0,且2(x-3)≠0,
∴x+1=0,
解得x=-1.
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
下列说法不正确的是( )
A、10的平方根是±
| ||||
| B、-2是4的一个平方根 | ||||
C、
| ||||
| D、实数与数轴上的点一一对应 |
方程x2-3x=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定是否有实数根 |
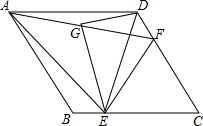 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.  如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E. 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF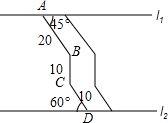 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.