题目内容
10. 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
分析 由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,由直角三角形的性质得出B1B2=$\frac{1}{\sqrt{3}}$A1B1=$\frac{\sqrt{3}}{3}$,A2B2=$\frac{1}{2}$A1B2=B1B2=$\frac{\sqrt{3}}{3}$,由相似多边形的性质得出正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积=$\frac{1}{3}$,求出正六边形A1B1C1D1E1F1的面积=$\frac{3\sqrt{3}}{2}$,得出正六边形A2B2C2D2E2F2的面积,同理得出正六边形A4B4C4D4E4F4的面积.
解答 解:由正六边形的性质得:∠A1B1B2=90°,∠B1A1B2=30°,A1A2=A2B2,
∴B1B2=$\frac{1}{\sqrt{3}}$A1B1=$\frac{\sqrt{3}}{3}$,
∴A2B2=$\frac{1}{2}$A1B2=B1B2=$\frac{\sqrt{3}}{3}$,
∵正六边形A1B1C1D1E1F1∽正六边形A2B2C2D2E2F2,
∴正六边形A2B2C2D2E2F2的面积:正六边形A1B1C1D1E1F1的面积=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$,
∵正六边形A1B1C1D1E1F1的面积=6×$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∴正六边形A2B2C2D2E2F2的面积=$\frac{1}{3}$×$\frac{3\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
同理:正六边形A4B4C4D4E4F4的面积=($\frac{1}{3}$)3×$\frac{3\sqrt{3}}{2}$=$\frac{\sqrt{3}}{18}$;
故答案为:$\frac{\sqrt{3}}{18}$.
点评 本题考查了正六边形的性质、相似多边形的性质、正六边形面积的计算等知识;熟练掌握正六边形的性质,由相似多边形的性质得出规律是关键.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)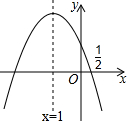 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论: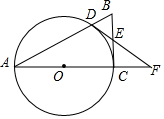 如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F. 如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.
如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度. 如图,在?ABCD中,已知点E和点F分别在AD和BC上,且DE=BF,连接CE和AF,试说明四边形AFCE是平行四边形.
如图,在?ABCD中,已知点E和点F分别在AD和BC上,且DE=BF,连接CE和AF,试说明四边形AFCE是平行四边形.