题目内容
正六边形的内切圆与它的外接圆的周长比是 ，面积比是 ．
考点：正多边形和圆
专题：
分析：根据垂径定理得出正六边形的内切圆与它的外接圆的半径，根据相似多边形的性质可得出周长之比等于半径之比，面积之比等于半径之比的平方．
解答：解：设正六边形的边长为2x，
则正六边形的内切圆的半径为
x，它的外接圆的半径为2x，
∴周长比是
x：2x=
：2，
面积比是3：4．
故答案为
：2，3：4．
则正六边形的内切圆的半径为
| 3 |
∴周长比是
| 3 |
| 3 |
面积比是3：4．
故答案为
| 3 |
点评：本题考查了正多边形和圆，明确正六边形的内切圆与它的外接圆的周长比等于半径之比，面积之比等于半径之比的平方是解此题的关键．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
在平面直角坐标系中有两点A（-2，2）、B（3，2），P是坐标轴上一点，若△ABP是直角三角形，则P点坐标分别是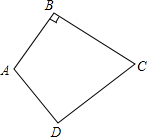
如图，有一张四边形纸片ABCD，AB=AD=6cm，CB=CD=8cm，且∠B=90°．
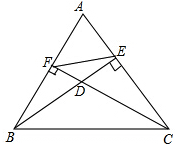如图，BE、CF分别是△ABC的边AC、AB上的高，BE与CF相交于点D，求证：
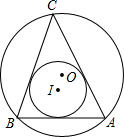如图，在△ABC中，AB=5，AC=8，∠CAB=60°，求△ABC的内切圆⊙I的半径和外接圆⊙O的半径．