题目内容
2．
如图，∠1=∠2，∠B=∠D，求证：AB=CD．
分析 已知条件∠1=∠2，∠B=∠D，再有公共边AC=CA可利用AAS证明△ABC≌△CDA根据全等三角形的性质可得AB=CD．
解答 证明：在△ABC和△CDA中，
$\left\{\begin{array}{l}{∠1=∠2}\\{∠B=∠D}\\{AC=AC}\end{array}\right.$，
∴△ABC≌△CDA（AAS），
∴AB=CD．
点评 此题主要考查了全等三角形的判定与性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
相关题目
已知：如图，求作△ABC的高AD、角平分线BE、中线CF．
13．下列命题正确的个数是（ ）
①一组对角相等，一组对边平行的四边形是平行四边形；
②有两条边和第三条边上的中线对应相等的两个三角形全等；
③对角线垂直相等的四边形是正方形；
④圆的切线垂直于圆的半径．
①一组对角相等，一组对边平行的四边形是平行四边形；
②有两条边和第三条边上的中线对应相等的两个三角形全等；
③对角线垂直相等的四边形是正方形；
④圆的切线垂直于圆的半径．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．
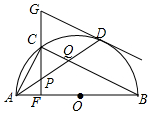如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CF⊥AB于点E，过点D的切线交FC的延长线于点G，连接AD，分别交CF、CB于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②AD=CB；③点P是△ACQ的外心；④GP=GD；⑤CB∥GD．其中正确结论的序号是（ ）
如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CF⊥AB于点E，过点D的切线交FC的延长线于点G，连接AD，分别交CF、CB于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②AD=CB；③点P是△ACQ的外心；④GP=GD；⑤CB∥GD．其中正确结论的序号是（ ）| A． | ①②④ | B． | ②③⑤ | C． | ③④ | D． | ②⑤ |
7．
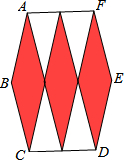如图，3个全等的菱形按如图方式拼合在一起，恰好得到一个边长相等的六边形，则菱形较长的对角线与较短的对角线之比是（ ）
如图，3个全等的菱形按如图方式拼合在一起，恰好得到一个边长相等的六边形，则菱形较长的对角线与较短的对角线之比是（ ）| A． | $\sqrt{15}$ | B． | $\sqrt{10}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
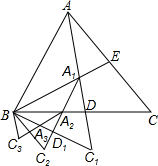已知如图，△ABC是面积为1的正三角形，AC和BC两边上的高BE与AD相交于点A1，延长AD到C1，使C1D=A1D，连接BC1，得△A1BC1，作其BC1边上的高A1D1交BD于A2，延长A1D1到C2，使A2D1=C2D1，连接BC2，得△A2BC2，有同样的方法得△A3BC3…当AnB与AB第一次重合时，△AnBCn的面积是$\frac{1}{{3}^{12}}$．
如图，直线A1B∥AnD，求证：∠A1+∠A2+∠A3+∠A4…∠An=（n-1）•180°．