题目内容
12.如图①,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.(1)请直接写出△ABC的面积;
(2)在图②中画出一个等腰△DEF,而且要使S△DEF=S△ABC,△DEF的三个顶点均与小正方形的顶点重合.
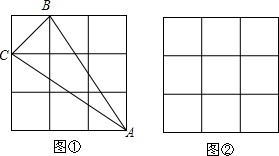
分析 (1)利用△ABC的面积=正方形的面积-三个直角三角形的面积计算即可;
(2)由(1)中的△ABC面积数值结合勾股定理即可得到△DEF.
解答 解:(1)△ABC的面积=9-$\frac{1}{2}$×1×1-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×3=2.5;
(2)如图所示:
点评 此题主要考查了勾股定理,以及复杂作图,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
2.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是( )
| A. | 5 | B. | 7 | C. | 5或7 | D. | 10 |
17.在正五边形、正六边形、正七边形、正八边形中,若只用同一种正多边形铺满地面,则可供选择的正多边形为( )
| A. | 正五边形 | B. | 正六边形 | C. | 正七边形 | D. | 正八边形 |
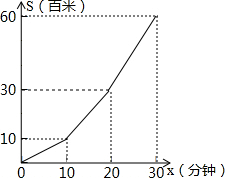 小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.
小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.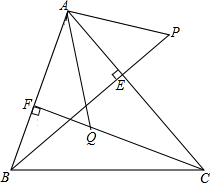 如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.