题目内容
18.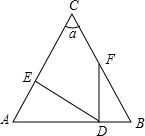 如图,∠A=∠B,∠C=α,DE⊥AC于点E,FD⊥AB于点D,探索∠EDF与α的关系,并说明理由.
如图,∠A=∠B,∠C=α,DE⊥AC于点E,FD⊥AB于点D,探索∠EDF与α的关系,并说明理由.
分析 利用等角的余角相等和已知角可求出∠EDB的数,从而可求得∠EDF的度数.
解答 解:∠EDF=90°-$\frac{1}{2}$α.
理由:∵∠A=∠B,∠C=α
∴∠A=∠B=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∵DE⊥AC于点E,FD⊥AB于点D,
∴∠AED=∠FDB=90°
∴∠EDA=∠BFD=90°-(90°-$\frac{1}{2}$α)=$\frac{1}{2}$α,
∴∠EDF=90°-∠EDA=90°-$\frac{1}{2}$α=.
点评 本题综合考查等腰三角形与等边三角形的性质及三角形外角性质等知识.一般是利用等腰三角形的性质得出有关角的度数,进而求出所求角的度数.

练习册系列答案
相关题目
9.下列各数+(-4),-(+$\frac{1}{4}$),-[+(-$\frac{1}{4}$)],+[-(+$\frac{1}{4}$)],+[-(-4)]中,正数有( )
| A. | 0个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列式子成立的是( )
| A. | xy2-2y2•x=-xy2 | B. | 3a+5b=8ab | C. | 3ab-ab=2 | D. | a3•a2=a6 |
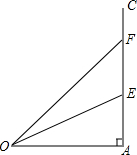 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.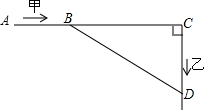 如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km?
如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km?