题目内容
18.解方程:(1)$\frac{2}{x-2}$-$\frac{1}{x}$=0
(2)$\frac{x-2}{x+2}-\frac{16}{{{x^2}-4}}=1$
(3)(2x+1)2-5=0
(4)(x-3)2+2x(x-3)=0.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)方程变形后,利用平方根定义开方即可求出解;
(4)方程利用因式分解法求出解即可.
解答 解:(1)去分母得:2x-x+2=0,
解得:x=-2,
经检验x=-2是分式方程的解;
(2)去分母得:x2-4x+4-16=x2-4,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
(3)方程整理得:(2x+1)2=5,
开方得:2x+1=±$\sqrt{5}$,
解得:x1=$\frac{-1+\sqrt{5}}{2}$,x2=$\frac{-1-\sqrt{5}}{2}$;
(4).分解因式得:(x-3)(3x-3)=0,
解得:x1=3,x2=1.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.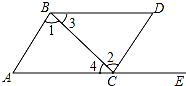 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠B=∠2 |
3.在等边三角形,正方形,直角三角形,平行四边形中,既是轴对称图形又是中心对称图形的是( )
| A. | 正方形 | B. | 等边三角形 | C. | 直角三角形 | D. | 平行四边形 |
 如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,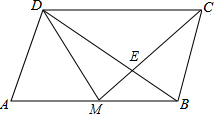 如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求:
如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求: 如图,平行四边形ABCD的对角线相交于点O,OE⊥BD交AD于点E,若BC=10cm,AB=7cm,则△ABE的周长是17cm.
如图,平行四边形ABCD的对角线相交于点O,OE⊥BD交AD于点E,若BC=10cm,AB=7cm,则△ABE的周长是17cm.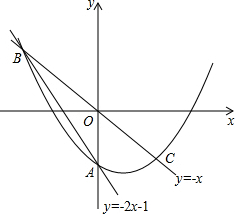 在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.
在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.