题目内容

10．阅读与计算：阅读以下材料．并完成相应的任务．
欧拉，瑞士数学家和物理学家、近代数学先驱之一．小时候放学回家常帮父亲放羊，一边放羊，一边读书，有一天，他发现羊的数量越来越多，达到了100只，羊圈很拥挤．后来，欧拉的父亲就规划出了面积刚好为600平方米的土地修建新羊圈，平均每只羊刚好占地6平方米，即将动工时发现用来作圈栏的篱笆只有100米长，若按原计划建羊圈，就要再添10米长的材料：要是缩小面积，每只羊的占地面积将会小于6平方米．此时，见父亲一脸无奈，小欧拉却对父亲水：“不用增加材料，也不用缩小羊圈，我还能使羊圈的面积达到最大”．
你能用二次函数的知识解释欧拉是如何修建羊圈，并使羊圈的面积最大的？

分析 设出羊圈的长和宽，列出羊圈的面积，然后将式子化为顶点式，即可求得面积的最大值，从而可以解答本题．

解答 解：设羊圈的长为x米，则宽为（50-x）米
S=x（50-x）=-x2+50x=-（x-25）2+625，
即x=25时，S取得最大值，此时，S=625，
即欧拉设计的羊圈的长和宽都为25米，则材料不用增加，面积达到了最大值625大于600．

点评 本题考查二次函数的应用，解题的关键是根据题目中的信息列出面积的表达式，与二次函数的顶点式联系起来．

练习册系列答案
相关题目
20．下列各式运算正确的是（　　）
A．（a-2）（2+a）=22-a2B．（x+2）（2x-2）=2x2-4C．（-a-b）（a+b）=a2-b2D．（ab-3）（ab+3）=a2b2-9
1．如图，点A，B，C在⊙O上，⊙O的半径为9，弧AB的长为2π，则∠ACB的大小是（　　）
A．20°B．45°C．60°D．40°
18．如图，在△ABC中，D为AB的中点，F为BC上一点，DF∥AC，延长FD至E，且DE=DF，联结AE、AF．
（1）求证：∠E=∠C；
（2）如果DF平分∠AFB，求证：AC⊥AB．
5．成都某电影院近日播放了一部爱国主义电影，针对学校师生特别推出的活动是：教师票60元，学生票20元．同时，根据师生购票数量的不同，还制定了如下可供选择的购票方案（要求只能选择以下两种方案中的一种方案购票）：
方案一：无论学生多少，10人内教师带领学生观看，所有教师不购票，但所有学生需要购买每人20元的个人票；
方案二：当师生总人数超过100人时，师生都购票但总票价九折优惠，且要求按整十数量购票，具体如下：
当师生总人数超过100人但不超过110人时，需按110人购票
当师生总人数超过110人但不超过120人时，需按120人购票
当师生总人数超过120人但不超过130人时，需按130人购票
…
某学校有5位老师带领全体七年级学生x人（175＜x≤195）到电影院观看本部电影．
（1）如果该校七年级学生人数为178人，试问应采用方案一和方案二中的哪种方案师生购票费用更省？
（2）如果采用方案一师生购票的费用和采用方案二师生购票的最省费用一样多，求该校七年级学生人数．
（3）如果该校七年级学生人数为x人，请用含x的代数式表示该校师生购票至少应付多少元？（直接写出结果，不必写解答过程．）
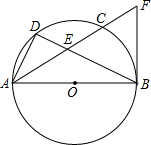15．如图，AB是⊙O的直径，点D是弧AC的中点，弦AC与BD相交于点E，DE=3，EB=6．
（1）求证：△ABD∽△EAD；
（2）求tan∠ABD的值；
（3）若点F是弦AC的延长线上一点，且△ABF的面积为18$\sqrt{3}$，求证：BF是⊙O的切线．
2．已知抛物线y=x2+bx+c的对称轴l交x轴于点A．
（1）若此抛物线经过点（1，2），当点A的坐标为（2，0）时，求此抛物线的解析式；
（2）抛物线y=x2+bx+c交y轴于点B，将该抛物线平移，使其经过点A，B，且与x轴交于另一点C，若b2=2c，b≤-1，设线段OB，OC的分别为m，n，试比较m与n+$\frac{3}{2}$的大小，并说明理由．
16．已知方程组$\left\{\begin{array}{l}{2x+y=1-m}\\{x+2y=2}\end{array}\right.$的解x、y满足x+y＞2，求m的取范围．
17．如图，若校门的坐标为（1，1），则实验楼的坐标是（3，3）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网