题目内容
1．
如图，点A，B，C在⊙O上，⊙O的半径为9，弧AB的长为2π，则∠ACB的大小是（ ）| A． | 20° | B． | 45° | C． | 60° | D． | 40° |
分析 连接AO、BO，然后根据弧AB的长为2π，求出圆心角∠AOB的度数，然后根据圆周角定理求出∠ACB的度数．
解答 解：连接AO、BO，
∵弧AB的长为2π，
∴2π=$\frac{nπ×9}{180}$，
解得：n=40°，
则∠ACB=$\frac{1}{2}$×40°=20°．
故选A．
点评 本题考查了弧长的计算，解答本题的关键是掌握弧长公式：l=$\frac{nπr}{180}$．
练习册系列答案
相关题目
11．
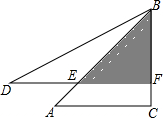将一副三角板（一个等腰直角三角形和一个锐角为60°的直角三角形）如图所示叠放在一起，若DB=20，则阴影部分的面积为（ ）
将一副三角板（一个等腰直角三角形和一个锐角为60°的直角三角形）如图所示叠放在一起，若DB=20，则阴影部分的面积为（ ）| A． | 50 | B． | 100 | C． | 150 | D． | 200 |
12．如果|a|=3，|b|=2，且a-b＜0．那么a+b的值是（ ）
| A． | -1，-5 | B． | 1，5 | C． | ±5 | D． | ±1 |
9．方程4x2-8x-25=0的一次项系数和常数项分别为（ ）
| A． | -2，25 | B． | -2，-25 | C． | 8，-25 | D． | -8，-25 |
16．下列关于有理数加减法表示正确的是（ ）
| A． | a＞0 b＜0，并且|a|＞|b|，则a+b=|a|+|b| | B． | a＜0 b＞0，并且|a|＞|b|，则a+b=|a|-|b| | ||
| C． | a＜0 b＞0，并且|a|＜|b|，则a-b=|b|+|a| | D． | a＜0 b＜0，并且|a|＞|b|，则a-b=|b|-|a| |
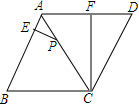如图，在菱形ABCD中，点P在对角线AC上，且PC=2PA，PE⊥AB于E，CF⊥AD于F，PE=2，求CF的长．
如图，抛物线y=$\frac{1}{4}$x2-$\frac{5}{4}$x+1与x轴的正半轴相交于点A，B（点A位于点B的左侧），与y轴的正半轴交于点．