题目内容
3.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边AB于点E.(1)点F为BC的中点,连接EF,(如图1),求证:EF是⊙O的切线;
(2)连接EO并延长交BC的延长线于点D,若⊙O的半径为3,∠EAC=60°(如图2),求AD的长.
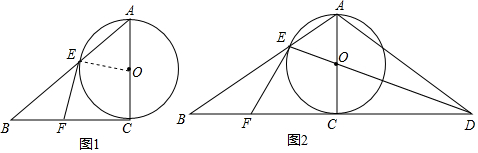
分析 (1)连结CE,求出EF=CF=BF,推出∠1+∠3=∠2+∠4,求出∠ACB=∠OEF=90°,根据切线的判定推出即可.
(2)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
解答 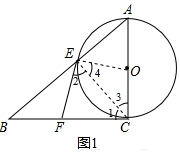 (1)证明:连结OE,CE,
(1)证明:连结OE,CE,
∵AC是直径,
∴∠AEC=90°,
∴∠BEC=90°,
∵F是BC的中点,
∴EF=$\frac{1}{2}$BC=FC,
∴∠1=∠2.
∵OC=OE,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠ACB=∠OEF,
∵∠ACB=90°,
∴∠OEF=90°,
又∵OE是半径,
∴EF是⊙O的切线.
(2)如图2,∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴∠EOA=60°,
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=3$\sqrt{3}$
∵在Rt△ACD中,∠ACD=90°,
CD=3$\sqrt{3}$,AC=6,
∴AD=3$\sqrt{7}$.
点评 本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,熟练掌握定理是解题的关键.

练习册系列答案
相关题目
 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题: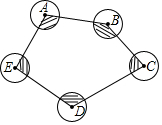 如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.
如图,⊙A、⊙B、⊙C、⊙D、⊙E的半径都是4cm,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)面积的和为24πcm2.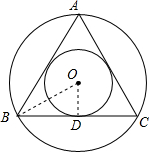 已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.
已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.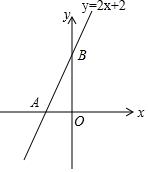 如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.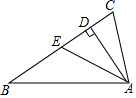 如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数.
如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数.