题目内容
16. 如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )| A. | y=$\frac{3}{x}$(x>0) | B. | y=$\frac{1}{x}$(x>0) | C. | y=$\frac{{\sqrt{3}}}{x}$(x>0) | D. | y=$\frac{1}{3x}$(x>0) |
分析 首先设B点坐标满足的函数解析式是y=$\frac{k}{x}$,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=2:1,继而求得答案.
解答  解:设B点坐标满足的函数解析式是y=$\frac{k}{x}$,
解:设B点坐标满足的函数解析式是y=$\frac{k}{x}$,
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=($\frac{OA}{OB}$)2,
∵AO=$\sqrt{3}$BO,
∴S△AOC:S△BOD=3,
∵S△AOC=$\frac{1}{2}$OC•AC=$\frac{3}{2}$,S△BOD=$\frac{1}{2}$,
∴设B点坐标满足的函数解析式是y=$\frac{1}{x}$.
故选B.
点评 此题考查了相似三角形的判定与性质以及反比例函数的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
6.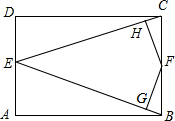 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{2}$$\sqrt{10}$ | C. | $\frac{3}{10}$$\sqrt{10}$ | D. | $\frac{3}{5}$$\sqrt{10}$ |
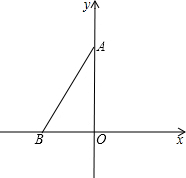 如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).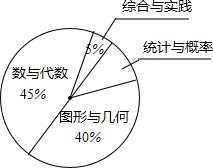 在结束了初中阶段数学内容的新课教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制了如图所示的扇形统计图,则唐老师安排复习“统计与概率”内容的时间为6课时.
在结束了初中阶段数学内容的新课教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制了如图所示的扇形统计图,则唐老师安排复习“统计与概率”内容的时间为6课时.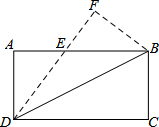 如图,矩形ABCD的边长AB=8,AD=4,若将△DCB沿BD所在直线翻折,点C落在点F处,DF与AB交于点E.则cos∠ADE=$\frac{4}{5}$.
如图,矩形ABCD的边长AB=8,AD=4,若将△DCB沿BD所在直线翻折,点C落在点F处,DF与AB交于点E.则cos∠ADE=$\frac{4}{5}$. 边长为1的正方形ABCD在平面直角坐标系中位置如图所示,以对角线BD为边作正方形BC1D1D,再以对角线BD1为边作正方形BB1C2D1,再以对角线B1D1为边作正方形B1C3D2D1,…按此规律做第10次所得正方形的顶点C10的坐标为(63,32).
边长为1的正方形ABCD在平面直角坐标系中位置如图所示,以对角线BD为边作正方形BC1D1D,再以对角线BD1为边作正方形BB1C2D1,再以对角线B1D1为边作正方形B1C3D2D1,…按此规律做第10次所得正方形的顶点C10的坐标为(63,32).