题目内容
6.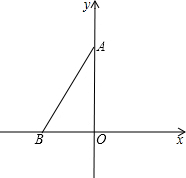 如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
分析 通过解直角三角形OAB求得点A的坐标.然后由等腰三角形的性质来求点P的坐标:分AB=AP和PB=AP两种情况.
解答 解:如图,∵点B的坐标为(-1,0),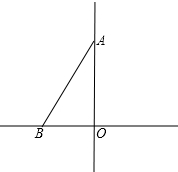 ∴OB=1.
∴OB=1.
又∵∠BAO=30°,
∴AB=2,OA=$\sqrt{3}$,
∴A(0,$\sqrt{3}$),
①当AB=AP时,点P的坐标为(0,2+$\sqrt{3}$);
②当PB=AP时,设P(0,a),则
(0+1)2+a2=(a-$\sqrt{3}$)2,
解得a=$\frac{\sqrt{3}}{3}$,则点P的坐标为(0,$\frac{\sqrt{3}}{3}$).
综上所述,符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
故答案是:(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
点评 本题考查了坐标与图形的性质,等腰三角形的判定.解题中利用等腰三角形的判定来解决特殊的实际问题,其关键是根据题意,结合图形,再利用数学知识来求解.

练习册系列答案
相关题目
17.已知-0.5xa+bya-b与$\frac{2}{3}{x}^{a-1}{y}^{3}$是同类项,那么( )
| A. | $\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ |
14.从-1、-2、3、4这四个数中,随机抽取两个数相乘,积为负数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
18.若∠A=35°16′,则其余角的度数为( )
| A. | 54°44′ | B. | 54°84′ | C. | 55°44′ | D. | 144°44′ |
16. 如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
 如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
如图,点A在反比例函数y=-$\frac{3}{x}$(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )| A. | y=$\frac{3}{x}$(x>0) | B. | y=$\frac{1}{x}$(x>0) | C. | y=$\frac{{\sqrt{3}}}{x}$(x>0) | D. | y=$\frac{1}{3x}$(x>0) |