Question

4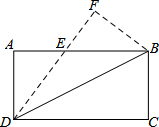．如图，矩形ABCD的边长AB=8，AD=4，若将△DCB沿BD所在直线翻折，点C落在点F处，DF与AB交于点E．则cos∠ADE=$\frac{4}{5}$．

Answer 1

分析 根据翻折的性质可得∠1=∠2，再根据两直线平行，内错角相等可得∠1=∠3，然后求出∠2=∠3，再根据等角对等边可得BF=DF，再表示出AF，然后在Rt△ABF中，利用勾股定理列出方程求出DF，根据余弦三角函数的定义即可求得答案．

解答 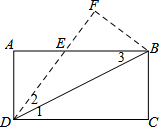解：如图，由翻折的性质得，∠1=∠2，∠F=∠C=90°，FB=BC=4，
∵矩形ABCD的边AB∥DC，
∴∠1=∠3，
∴∠2=∠3，
∴BE=DE，
∵AB=8，
∴AE=8-BE，
在Rt△ABE中，AD²+AE²=DE²，
∴4²+（8-BE）²=BE²，
解得BE=5，
∴cos∠ADE=$\frac{FB}{BE}$=$\frac{4}{5}$．

点评 本题考查了翻折变换的性质，平行线的性质，矩形的性质，三角函数的定义，勾股定理的应用，熟练掌握翻折前后的两个图形能够完全重合是解题的关键．