Question

6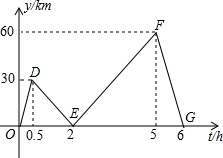．甲、乙两人分别开汽车和摩托车从A地出发沿同一条公路匀速前往B地，乙出发半小时后甲出发，设乙行驶的时间t（h），甲、乙两人之间的距离为y（km），y与t之间关系的图象如图所示．
（1）分别指出点E，F所表示的实际意义；
（2）分别求出线段DE，FG所在直线的函数表达式；
（3）分别求甲、乙两人行驶的速度．

Answer 1

分析 （1）根据图象中的信息即可得到结论；
（2）设直线DE的函数表达式为y=kx+b，直线FG的函数表达式为y₁=k₁x+b₁，列方程组即可得到结论；
（3）设甲的速度为v_甲km/h，甲的速度为v乙km/h，根据图象信息得方程组即可得到结论．

解答 解：（1）点E表示的实际意义是甲、乙两人在乙出发2小时时相遇，此时两人之间的距离为0，F所表示的实际意义乙出发5小时时甲到达B地，此时两人之间的距离为60km；
（2）设直线DE的函数表达式为y=kx+b，
把（0.5，30），（2，0）代入得$\left\{\begin{array}{l}{0.5k+b=30}\\{2k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-20}\\{b=40}\end{array}\right.$，
则直线DE的函数表达式为y=-20x+40，
设直线FG的函数表达式为y₁=k₁x+b₁，把（5，60），（6，0）代入得$\left\{\begin{array}{l}{5{k}_{1}+{b}_{1}=60}\\{6{k}_{1}+{b}_{1}=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{k}_{1}=-60}\\{{b}_{1}=360}\end{array}\right.$，∴直线FG的函数表达式为y₁=-60x+360；
（3）设甲的速度为v_甲km/h，甲的速度为v乙km/h，
根据图象得$\left\{\begin{array}{l}{（2-0.5）{v}_{甲}-2{v}_{乙}=0}\\{（5-0.5）{v}_{甲}=-5{v}_{乙}=60}\end{array}\right.$，解得：$\left\{\begin{array}{l}{{v}_{甲}=80}\\{{v}_{乙}=60}\end{array}\right.$，
答：甲行驶的速度是80km/h，乙行驶的速度是60km/h．

点评 本题考查了一次函数的应用，解决本题的关键是根据图象获取相关信息，利用待定系数法求函数解析式．