题目内容

11．解不等式组$\left\{\begin{array}{l}{2x-1＜4}\\{\frac{x-1}{2}≤x+1}\end{array}\right.$．

分析 首先解每个不等式，然后把每个不等式的解集的公共部分就是不等式组的解集．

解答 解：$\left\{\begin{array}{l}{2x-1＜4…①}\\{\frac{x-1}{2}≤x+1…②}\end{array}\right.$，
解①得x＜$\frac{5}{2}$，
解②得x≥-3．
则不等式组的解集是-3≤x＜$\frac{5}{2}$．

点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．

练习册系列答案
相关题目
1．若规定精确到1，那么$\sqrt{60}$的估算值为（　　）
A．3B．7C．8D．7或8
2．已知关于x的一元二次方程mx2+2x-1=0（m为常数）有两个不相等的实数根，则m的取值范围是m＞-1且m≠0．
19．在建设国家旅游综合改革实验区和大枣国际旅游胜地的背景中，桂林旅游业正在实施转型升级，据报道，今年我市旅游业资金投入将比2013年增长680000000元推动着桂林旅游呈现出多点开花，亮点纷呈的局面，用科学记数法表示680000000元为6.8×108元．
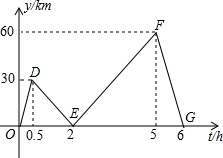6．甲、乙两人分别开汽车和摩托车从A地出发沿同一条公路匀速前往B地，乙出发半小时后甲出发，设乙行驶的时间t（h），甲、乙两人之间的距离为y（km），y与t之间关系的图象如图所示．
（1）分别指出点E，F所表示的实际意义；
（2）分别求出线段DE，FG所在直线的函数表达式；
（3）分别求甲、乙两人行驶的速度．
16．（1）解方程：x2=3（x+1）．
（2）用配方法解方程：x2-2x-24=0．
3．下列运算中正确的是（　　）
A．a5÷a5=0B．a6×a4=a24C．（x2-y2）2=x4-y4D．（x3）3=x9
20．已知抛物线y=-x2+bx+c与直线y=-4x+m相交于第一象限不同的两点，A（5，n），B（e，f）
（1）若点B的坐标为（3，9），求此抛物线的解析式；
（2）将此抛物线平移，设平移后的抛物线为y=-x2+px+q，过点A与点（1，2），且m-q=25，在平移过程中，若抛物线y=-x2+bx+c向下平移了S（S＞0）个单位长度，求S的取值范围．
1．凯里市某文具店某种型号的计算器每只进价12元，售价20元，多买优惠，优惠方法是：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降价0.1元，例如：某人买18只计算器，于是每只降价0.1×（18-10）=0.8（元），因此所买的18只计算器都按每只19.2元的价格购买，但是每只计算器的最低售价为16元．
（1）求一次至少购买多少只计算器，才能以最低价购买？
（2）求写出该文具店一次销售x（x＞10）只时，所获利润y（元）与x（只）之间的函数关系式，并写出自变量x的取值范围；
（3）一天，甲顾客购买了46只，乙顾客购买了50只，店主发现卖46只赚的钱反而比卖50只赚的钱多，请你说明发生这一现象的原因；当10＜x≤50时，为了获得最大利润，店家一次应卖多少只？这时的售价是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网