题目内容
已知a=|x-5|+|x-2|+|x+3|，求当x= 时，a有最小值为 ．
考点：绝对值
专题：分类讨论
分析：利用绝对值的性质得出当x取到使|x-5|=0，|x-2|=0，|x+3|=0的中间值时，其和最小，进而得出答案．
解答：解：∵a=|x-5|+|x-2|+|x+3|，
∴x=2时，a最小，
故a=3+0+5=8．
故答案为：2，8．
∴x=2时，a最小，
故a=3+0+5=8．
故答案为：2，8．
点评：此题主要考查了绝对值的性质，得出x取到中间值时其和最小进而求出是解题关键．
练习册系列答案
相关题目
如图，点B是线段AC上的一点，分别以AB、BC、CA为直径作半圆，求证：半圆AB的长与半圆BC的长之和等于半圆AC的长．
如图所示，在△ABC中，I是内角平分线AD、BE、CF的交点，过点I作IG⊥BC于点G，试问：∠DIG与∠GIC相等吗？为什么？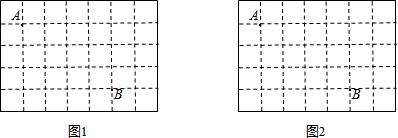
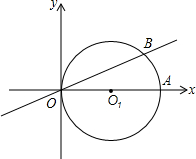如图，在平面直角坐标系中圆O1的圆心在x轴上，直径OA=2，直线OB交圆O1于B，且∠BOA=15°