题目内容
 如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.考点:圆的认识
专题:证明题
分析:根据圆的周长公式可计算出半圆AB的长=
πAB,半圆BC的长=
πBC,半圆AC的长=
πAC,则半圆AB的长+半圆BC的长=
π•(AB+BC)=
π•AC,即半圆AB的长与半圆BC的长之和等于半圆AC的长.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵半圆AB的长=
•2π•
=
πAB,半圆BC的长=
•2π•
=
πBC,半圆AC的长=
•2π•
=
πAC,
∴半圆AB的长+半圆BC的长=
πAB+
πBC=
π•(AB+BC),
∵AB+BC=AC,
∴半圆AB的长+半圆BC的长=
π•AC,
∴半圆AB的长与半圆BC的长之和等于半圆AC的长.
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
∴半圆AB的长+半圆BC的长=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB+BC=AC,
∴半圆AB的长+半圆BC的长=
| 1 |
| 2 |
∴半圆AB的长与半圆BC的长之和等于半圆AC的长.
点评:本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知二次函数y=2x2+m(m为常数).
已知二次函数y=2x2+m(m为常数).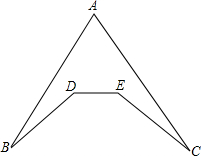 某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线.
某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线. 如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是
如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是