题目内容
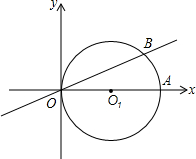 如图,在平面直角坐标系中圆O1的圆心在x轴上,直径OA=2,直线OB交圆O1于B,且∠BOA=15°
如图,在平面直角坐标系中圆O1的圆心在x轴上,直径OA=2,直线OB交圆O1于B,且∠BOA=15° (1)求直线OB的解析式;
(2)求经过O、A、B三点的抛物线y=ax2+bx+c的表达式;
(3)动点Q从A点出发顺时针在半圆AQO上运动,速度为
| π |
| 9 |
考点:圆的综合题
专题:
分析:(1)连接BO1,可知∠BO1A=30°,过B作BC⊥OA于点C,可求得BC=
,O1C=
,可求出OC,从而可得出B点的坐标,再利用待定系数法可求出直线OB的解析式;
(2)可求出O、A点的坐标,可利用两点式,再把B点的坐标代入可求出抛物线的表达式;
(3)因为半径为1,当PQ=1时,则可知BQ过点P,此时∠PO1Q=150°,可求得弧AQ的长,再利用速度可求得时间.
| 1 |
| 2 |
| ||
| 2 |
(2)可求出O、A点的坐标,可利用两点式,再把B点的坐标代入可求出抛物线的表达式;
(3)因为半径为1,当PQ=1时,则可知BQ过点P,此时∠PO1Q=150°,可求得弧AQ的长,再利用速度可求得时间.
解答:解:
(1)如图1,连接BO1,
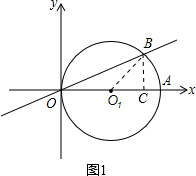
∴∠BOA=15°,
∴∠BO1A=2∠BOA=30°,
过B作BC⊥OA于点C,
∵OA=1,
∴O1B=1,
在Rt△O1BC中可求得BC=
,O1C=
,
∴OC=1+
,
∴B点坐标为(1+
,
),
设直线OB解析式为y=kx,则有
=(1+
)k,解得k=2-
,
∴直线OB的解析式为y=(2-
)x;
(2)∵OA=2,
∴A(0,2),且O(0,0),
设抛物线的解析式为y=ax(x-2),把B点坐标代入可得
=a(
+1)(
-1),解得a=-2,
∴抛物线解析式为y=-2x(x-2),即y=-2x2+4x;
(3)∵圆的半径为1,
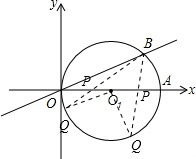
如图2,当P点在O1右侧时,∠PO1Q为锐角,此时PQ<O1Q,
当P点在O1左侧时,∠PO1Q为锐角,此时PQ<O1Q,
∴只有当点P在O1时,PQ=O1Q=1,即BQ过O1点,
此时∠QO1A=180°-∠AO1B=130°,
∴
的长为:
=
,
又Q点的速度为
长/秒,
∴Q点运动的时间为:
÷
=6.5(秒),
即当时间为6.5秒时,PQ的长为1.
(1)如图1,连接BO1,

∴∠BOA=15°,
∴∠BO1A=2∠BOA=30°,
过B作BC⊥OA于点C,
∵OA=1,
∴O1B=1,
在Rt△O1BC中可求得BC=
| 1 |
| 2 |
| ||
| 2 |
∴OC=1+
| ||
| 2 |
∴B点坐标为(1+
| ||
| 2 |
| 1 |
| 2 |
设直线OB解析式为y=kx,则有
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴直线OB的解析式为y=(2-
| 3 |
(2)∵OA=2,
∴A(0,2),且O(0,0),
设抛物线的解析式为y=ax(x-2),把B点坐标代入可得
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴抛物线解析式为y=-2x(x-2),即y=-2x2+4x;
(3)∵圆的半径为1,

如图2,当P点在O1右侧时,∠PO1Q为锐角,此时PQ<O1Q,
当P点在O1左侧时,∠PO1Q为锐角,此时PQ<O1Q,
∴只有当点P在O1时,PQ=O1Q=1,即BQ过O1点,
此时∠QO1A=180°-∠AO1B=130°,
∴
 |
| AQ |
| 130π |
| 180 |
| 13π |
| 18 |
又Q点的速度为
| π |
| 9 |
∴Q点运动的时间为:
| 13π |
| 18 |
| π |
| 9 |
即当时间为6.5秒时,PQ的长为1.
点评:本题主要考查待定系数法求函数解析式和圆周角定理、弧长的计算等知识的综合应用,掌握待定系数法是求函数解析的常用方法,在(1)(2)中求出B点的坐标是解题的关键;在(3)中确定出直线BQ的位置是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、有理数的绝对值都是正数 |
| B、0是单项式 |
| C、代数式分为单项式和多项式 |
| D、最小的整数是0 |
 如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm. 如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是
如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是