题目内容
已知a、b均为正数,且a≠b,则a2、2ab和b2是否一定能构成三角形?请说明理由.
考点:三角形边角关系
专题:探究型
分析:要想说明a2、2ab和b2不一定能构成三角形,只要找到满足条件的a、b,使得a2、2ab和b2中有两数之和小于第三个数即可.
解答:解:a2、2ab和b2不一定能构成三角形.
理由:当a=1,b=2时,a2=1,2ab=4,b2=4,
因为1+4>4,
所以1,4,4能构成三角形;
当a=1,b=3时,a2=1,2ab=6,b2=9,
因为1+6<9,
所以1,6,9不能构成三角形.
综上所述:当a、b均为正数,且a≠b时,a2、2ab和b2不一定能构成三角形.
理由:当a=1,b=2时,a2=1,2ab=4,b2=4,
因为1+4>4,
所以1,4,4能构成三角形;
当a=1,b=3时,a2=1,2ab=6,b2=9,
因为1+6<9,
所以1,6,9不能构成三角形.
综上所述:当a、b均为正数,且a≠b时,a2、2ab和b2不一定能构成三角形.
点评:本题主要考查的是三角形三边构成条件,要想说明一个命题不一定成立,只需举一个反例即可,而运用特值法进行验证则是解决本题的关键.

练习册系列答案
相关题目
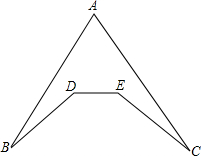 某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线.
某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线. 如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm. 如图所示,∠α,∠β分别是四边形ABCD的外角,求证:∠α+∠β=∠A+∠C.
如图所示,∠α,∠β分别是四边形ABCD的外角,求证:∠α+∠β=∠A+∠C.