题目内容
17.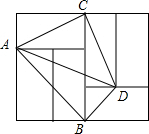 如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )
如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
分析 根据6个小矩形全等知DF=DG=BF=1、FG=AE=BE=2,在RT△BDF中BD=$\sqrt{2}$、∠DBF=45°,RT△ABE中AB=2$\sqrt{2}$、∠ABE=∠ABF=∠DBF=45°,进而知∠ABD=90°,在RT△ABD中根据勾股定理求得AD长,再根据正弦函数定义可得sin∠BAD的值.
解答 解:如图,根据题意知,DF=BF=DG=1,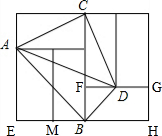
∴FG=AE=BE=2,∠DBF=45°,BD=$\sqrt{2}$,
∴AB=2$\sqrt{2}$,∠ABF=∠DBF=45°,
∴∠ABD=90°,
在RT△ABD中,∵AB=2$\sqrt{2}$,BD=$\sqrt{2}$,
∴AD=$\sqrt{10}$,
∴sin∠BAD=$\frac{BD}{AD}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
故选:A.
点评 本题考查了勾股定理,锐角三角函数的定义的应用,主要考查学生的理解能力和观察图形的能力,求三角函数值需构建直角三角形是解此类题的常用作法.

练习册系列答案
相关题目
7.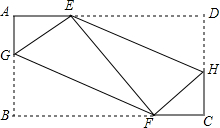 已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
 已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )
已知在矩形ABCD中,AB=4,AD=7,点G、F、H、E是分别边AB、BC、DC、AD上的点,分别沿HE,GF折叠矩形恰好使DE、BF都与EF重合,则AE=( )| A. | 1或$\frac{8}{3}$ | B. | 2或$\frac{8}{3}$ | C. | $\frac{3}{2}$或$\frac{8}{3}$ | D. | $\frac{5}{2}$或$\frac{8}{3}$ |
9.已知m是方程x2=x+1的一个根,则关于x的方程x2+2xm2-2xm-1=0有一个根是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | -1+$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
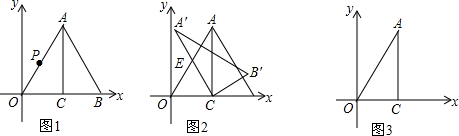
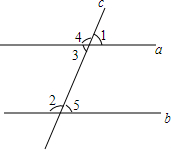 如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b.
如图,直线a,b被直线c所截,∠1+∠2=180°,试用三种方法说明a∥b.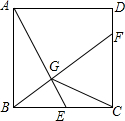 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.
如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.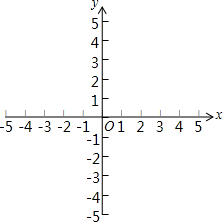 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义: