题目内容
15．不改变分式的值，使下列分式的分子、分母的最高次项的系数都是正数：（1）$\frac{2-a}{{a}^{2}-4}$
（2）$\frac{x-{x}^{2}}{2x-{x}^{2}-1}$．
分析 根据分子、分母、分式中有两个改变符号，分式的值不变进行变形即可．
解答 解：（1）$\frac{2-a}{{a}^{2}-4}$=-$\frac{a-2}{{a}^{2}-4}$；
（2）$\frac{x-{x}^{2}}{2x-{x}^{2}-1}$=$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$．
点评 此题考查了分式的基本性质，解题关键是：根据分子、分母、分式中有两个改变符号，分式的值不变进行变形即可．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
5．北京新国际机场采用“海星”设计方案，航站楼主体与五座向外伸展的指廊总建筑面积为1 030 000平方米，将1030000用科学记数法表示应为（ ）
| A． | 103×104 | B． | 10.3×105 | C． | 1.03×105 | D． | 1.03×106 |
20．
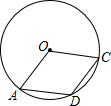如图，在半径为6的⊙O中，D是$\widehat{AC}$上一点，∠ADC=115°，则$\widehat{AC}$的长为（ ）
如图，在半径为6的⊙O中，D是$\widehat{AC}$上一点，∠ADC=115°，则$\widehat{AC}$的长为（ ）| A． | $\frac{23}{6}$π | B． | $\frac{23}{3}$π | C． | $\frac{13}{3}$π | D． | $\frac{13}{6}$π |
7．
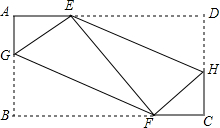已知在矩形ABCD中，AB=4，AD=7，点G、F、H、E是分别边AB、BC、DC、AD上的点，分别沿HE，GF折叠矩形恰好使DE、BF都与EF重合，则AE=（ ）
已知在矩形ABCD中，AB=4，AD=7，点G、F、H、E是分别边AB、BC、DC、AD上的点，分别沿HE，GF折叠矩形恰好使DE、BF都与EF重合，则AE=（ ）| A． | 1或$\frac{8}{3}$ | B． | 2或$\frac{8}{3}$ | C． | $\frac{3}{2}$或$\frac{8}{3}$ | D． | $\frac{5}{2}$或$\frac{8}{3}$ |
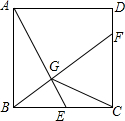如图，已知正方形ABCD的边长为2，E是BC边上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．则CG的最小值为$\sqrt{5}$-1．