题目内容
13.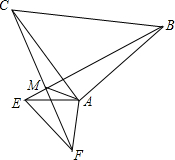 已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.
已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.(1)求证:BE=CF;
(2)求证AM平分∠BMF,并计算∠AME的度数.
分析 (1)求出∠EAB=∠FAC,根据SAS推出两三角形全等即可;
(2)过A作AQ⊥BE于Q,AH⊥CF于H,根据全等三角形性质和三角形面积求出AQ=AH,根据角平分线性质得出即可;根据三角形的内角和,可得∠CMB=∠BAC=78°,∠BMA=∠AMF,即可求出答案.
解答 (1)①解:∵∠BAC=∠EAF,
∴∠BAC+∠EAC=∠EAF+∠EAC,
∴∠EAB=∠FAC,
在△BAE和△CAF中
$\left\{\begin{array}{l}{AB=AC}\\{∠EAB=∠FAC}\\{AE=AF}\end{array}\right.$
∴△BAE≌△CAF(SAS).
BE=CF;
(2)证明:如图1: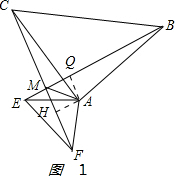
过A作AQ⊥BE于Q,AH⊥CF于H,
∵△BAE≌△CAF,
∴△BAE的面积=△CAF的面积,CF=BE,
∴$\frac{1}{2}$CF×AH=$\frac{1}{2}$BE×AQ,
∴AH=AQ,
∵AQ⊥BE,AH⊥CF,
∴AM平分∠BMF.
∵∠ABC+∠ACB=∠MBC+∠MCB=102°,
∴∠CMB=∠BAC=78°,AM平分∠BMF,
∴∠EMF=∠CMB=78°,∠BAM=180°-∠CMB=102°,
∠AMF=∠BMA=$\frac{1}{2}$∠BMF=$\frac{1}{2}$(180°-∠CMB)=$\frac{1}{2}$(180°-78)=90°-39°=51°,
∴∠AME=∠AMF+∠EMF=51°+78°=129°.
点评 本题考查了全等三角形的性质和判定,三角形外角性质,三角形的内角和定理,角平分线性质的应用,主要考查学生的推理能力,有一定的难度.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.下列计算正确的是( )
| A. | $\sqrt{16}=±4$ | B. | $\sqrt{8}-2\sqrt{2}=0$ | C. | $\sqrt{24}-\sqrt{4}$ | D. | $({2-\sqrt{5}})({2+\sqrt{5}})=1$ |
5.化简(-2)2015+22016,结果为( )
| A. | -2 | B. | 0 | C. | -22015 | D. | 22015 |
 把一块直尺与一块三角板如图放置,若∠1=35°,则∠2的度数为125°.
把一块直尺与一块三角板如图放置,若∠1=35°,则∠2的度数为125°. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=$\frac{3}{2}$或$\frac{12}{5}$s时,△PBQ为直角三角形.
如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=$\frac{3}{2}$或$\frac{12}{5}$s时,△PBQ为直角三角形.