题目内容
4. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=$\frac{3}{2}$或$\frac{12}{5}$s时,△PBQ为直角三角形.
如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=$\frac{3}{2}$或$\frac{12}{5}$s时,△PBQ为直角三角形.
分析 先分别表示出BP,BQ的值,当∠BQP和∠BPQ分别为直角时,由等边三角形的性质就可以求出结论.
解答  解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6-2x,BQ=x,
∴6-2x=2x,
解得x=$\frac{3}{2}$;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴x=2(6-2x),
解得x=$\frac{12}{5}$.
答:$\frac{3}{2}$或$\frac{12}{5}$秒时,△BPQ是直角三角形.
故答案为$\frac{3}{2}$或$\frac{12}{5}$.
点评 本题考查了等边三角形的性质的运用,30°角的直角三角形的性质的运用,勾股定理的运用,利用分类讨论是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知x=2是关于x的方程2ax-1=3的解,则a的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
12.下列函数式中,是二次函数的是( )
| A. | $y=\frac{x^2}{3}$ | B. | y=2x2+$\frac{1}{x}$ | C. | $y=\frac{1}{x^2}$ | D. | y=2x+3 |
9.下列图形:①三角形,②线段,③正方形,④直角、⑤圆,其中是轴对称图形的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
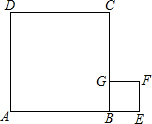 如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).
如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).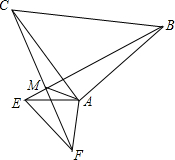 已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.
已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.