题目内容
3. 把一块直尺与一块三角板如图放置,若∠1=35°,则∠2的度数为125°.
把一块直尺与一块三角板如图放置,若∠1=35°,则∠2的度数为125°.
分析 根据三角形外角性质求出∠BCQ,根据平行线的性质得出∠2=∠BCQ,代入求出即可.
解答 解:
∵∠1=35°,∠A=90°,
∴∠BCQ=∠A+∠1=90°+35°=125°,
∵EF∥MN,
∴∠2=∠BCQ=125°,
故答案为:125°.
点评 本题考查了平行线的性质和三角形外角性质的应用,能求出∠2=∠BCQ是解此题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
2.下列关于圆的说法,正确的是( )
| A. | 相等的圆心角所对的弦相等 | |
| B. | 过圆心且平分弦的直线一定垂直于该弦 | |
| C. | 经过半径的端点且垂直于该半径的直线是圆的切线 | |
| D. | 相交两圆的连心线一定垂直且平分公共弦 |
15.已知x=2是关于x的方程2ax-1=3的解,则a的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
12.下列函数式中,是二次函数的是( )
| A. | $y=\frac{x^2}{3}$ | B. | y=2x2+$\frac{1}{x}$ | C. | $y=\frac{1}{x^2}$ | D. | y=2x+3 |
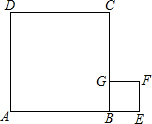 如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).
如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).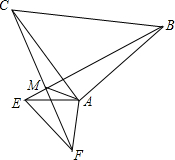 已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.
已知在△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF=78°,FC、BE相交于点M,连接AM.