题目内容
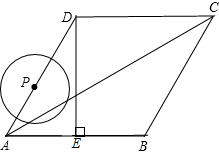 如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.
如图,在菱形ABCD中,∠BAD=60°,DE⊥AB于点E,且AE=2,动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.(1)求线段AD的长度;
(2)t为何值时,以点P为圆心、以1为半径的圆与DE相切?
(3)请你直接写出t为何值时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
| 3 |
考点:圆的综合题
专题:
分析:(1)由在菱形ABCD中,∠BAD=60°,DE⊥AB,AE=2,可求得∠ADE=30°,继而可求得线段AD的长度;
(2)由在菱形ABCD中,∠BAD=60°,易求得∠1=∠2=∠3=∠4=30°,AD=DC=CB=BA=4,然后分别从①点P在AD上与AC相切时,②点P在DC上与AC相切时,③点P在BC上与AC相切时,④点P在AB上与AC相切时,去分析求解即可求得答案;
(3)首先分析可得当⊙P过点A与C时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
,然后分别从点P在AD,DC,CB,BA上去分析求解,继而可求得答案.
(2)由在菱形ABCD中,∠BAD=60°,易求得∠1=∠2=∠3=∠4=30°,AD=DC=CB=BA=4,然后分别从①点P在AD上与AC相切时,②点P在DC上与AC相切时,③点P在BC上与AC相切时,④点P在AB上与AC相切时,去分析求解即可求得答案;
(3)首先分析可得当⊙P过点A与C时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
| 3 |
解答:解:(1)∵在菱形ABCD中,∠BAD=60°,DE⊥AB,AE=2,
∴∠ADE=90°-∠BAD=30°,
∴AD=2AE=4;
( 2)∵四边形ABCD是菱形,∠BAD=60°,
2)∵四边形ABCD是菱形,∠BAD=60°,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,AD=DC=CB=BA=4,
如图所示:
①点P在AD上与AC相切时,
连接P1F,则P1F⊥AC,P1F=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2;
②点P在DC上与AC相切时,CP2=2r=2,
∴AD+DP2=6,
∴t2=6;
③点P在BC上与AC相切时,CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10;
④点P在AB上与AC相切时,AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切.
 (3)如图2,⊙P过点A与点C,
(3)如图2,⊙P过点A与点C,
过点P作PN⊥AC于点N,
∵PA=1,∠DAC=30°,
∴PN=
PA=
,
∴AN=
=
,
∴AM=2AN=
,
∴当⊙P过点A与C时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
,
①当点P在AD上时,AP1=1,
即t1=1;
②当点P在DC上时,CP2=1,
即t2=AD+DC-CP2=4+4-1=7;
③当点P在CB上时,CP3=1,
即t3=AD+DC+CP3=4+4+1=9;
④当点P在BA上时,AP4=1,
即t4=AD+DC+BC+AB-AP4=4+4+4+4-1=15;
∴当t=1、7、9、15时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
.
∴∠ADE=90°-∠BAD=30°,
∴AD=2AE=4;
(
 2)∵四边形ABCD是菱形,∠BAD=60°,
2)∵四边形ABCD是菱形,∠BAD=60°,∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,AD=DC=CB=BA=4,
如图所示:
①点P在AD上与AC相切时,
连接P1F,则P1F⊥AC,P1F=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2;
②点P在DC上与AC相切时,CP2=2r=2,
∴AD+DP2=6,
∴t2=6;
③点P在BC上与AC相切时,CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10;
④点P在AB上与AC相切时,AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切.
 (3)如图2,⊙P过点A与点C,
(3)如图2,⊙P过点A与点C,过点P作PN⊥AC于点N,
∵PA=1,∠DAC=30°,
∴PN=
| 1 |
| 2 |
| 1 |
| 2 |
∴AN=
| PA2-PN2 |
| ||
| 2 |
∴AM=2AN=
| 3 |
∴当⊙P过点A与C时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
| 3 |
①当点P在AD上时,AP1=1,
即t1=1;
②当点P在DC上时,CP2=1,
即t2=AD+DC-CP2=4+4-1=7;
③当点P在CB上时,CP3=1,
即t3=AD+DC+CP3=4+4+1=9;
④当点P在BA上时,AP4=1,
即t4=AD+DC+BC+AB-AP4=4+4+4+4-1=15;
∴当t=1、7、9、15时,以点P为圆心、以1为半径的圆与对角线AC相交,所截得的弦长为
| 3 |
点评:此题考查了切线的性质、垂径定理、勾股定理、菱形的性质以及含30°角的直角三角形的性质等知识.此题综合性较强,难度较大,注意掌握辅助线的作法,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 2014年2月13日新疆于田县发生7.3级地震.地震救援队接到上级命令后立即赶赴震区进行救援.救援队利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B 相距4米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命所在点C的深度.(结果精确到0.1米,参考数据:
2014年2月13日新疆于田县发生7.3级地震.地震救援队接到上级命令后立即赶赴震区进行救援.救援队利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B 相距4米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命所在点C的深度.(结果精确到0.1米,参考数据: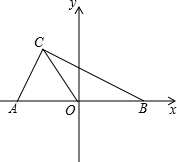 如图在平面直角坐标系中,A(a,0),B(b,0),(-1,2).且|2a+b+1|+
如图在平面直角坐标系中,A(a,0),B(b,0),(-1,2).且|2a+b+1|+ 我市某外资企业生产的一批产品上市后30天内全部售完.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如表.
我市某外资企业生产的一批产品上市后30天内全部售完.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如表. 如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.