题目内容
8. 如图,△ABC中,AC=BC,∠C=90°,直角顶点C(1,0),A(-1,4),则点B的坐标为(5,2).
如图,△ABC中,AC=BC,∠C=90°,直角顶点C(1,0),A(-1,4),则点B的坐标为(5,2).
分析 作BD⊥x轴于D点,作AE⊥x轴于点E,易证∠EAC=∠BCD,即可证明△EAC≌△DCB,可得CD=AE,BD=OE,即可解题.
解答 解:如图,作BD⊥x轴于D点,AE⊥x轴于点E,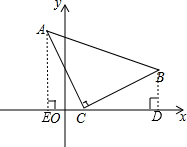
∵BD⊥x轴于D点,AE⊥x轴于点E,
∴∠AEC=∠CDB=90°,
∵∠C=90°,
∴∠ACE+∠BCD=90°,
∵∠ACE+∠EAC=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
$\left\{\begin{array}{l}{∠AEC=∠CDB}\\{∠EAC=∠BCD}\\{AC=BC}\end{array}\right.$
∴△AEC≌△CDB,
∴CD=AE,EC=BD,
∵点C(1,0),A(-1,4),
∴OC=1,OE=1,AE=4,
∴EC=2,
∴CD=4,BD=2,
∴OD=5,
∴点B的坐标为(5,2).
故答案为:(5,2).
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△EAC≌△DCB是解题的关键.

练习册系列答案
相关题目
20.2015年,号称“千湖之省”的湖北正遭受大旱,为提高学生的环保意识,节约用水,某校数学教师编造了一道应用题:为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水的收费作如下规定:
如某居民一月份用水9吨,则应收水费为:6×2+4×(9-6)=24(元)
(1)若该户居民3月份用水13吨,则应收水费52 元.
(2)若该户居民5、6月份共用水15吨(五月份用水超过六月份),共交水费44元,则该户居民5、6月份各用水多少吨?
| 月用水量(单位:吨) | 单价(单位:元/吨) |
| 不大于6吨部分 | 2 |
| 大于6吨且不大于10吨部分 | 4 |
| 大于10吨部分 | 8 |
(1)若该户居民3月份用水13吨,则应收水费52 元.
(2)若该户居民5、6月份共用水15吨(五月份用水超过六月份),共交水费44元,则该户居民5、6月份各用水多少吨?
 如图,E、F为线段AB上两点,AD∥CB,且AD=CB,∠D=∠C.求证:AF=BE.
如图,E、F为线段AB上两点,AD∥CB,且AD=CB,∠D=∠C.求证:AF=BE. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论: 如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.
如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.