题目内容
14.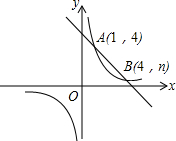 如图,直线AB与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,直线AB与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.(1)求反比例函数的解析式;
(2)是否存在x轴上的一个动点P,使PA+PB最小,若存在求出P点坐标,若不存在,请说明理由.
分析 (1)把A点坐标代入y=$\frac{m}{x}$中求出m即可得到反比例函数解析式;
(2)把B(4,n)代入y=$\frac{4}{x}$求出n得到B(4,1),作点A关于x轴的对称点A′,如图,则A′(1,-4),连结A′B交x轴于P,利用两点之间线段最短得到此时PA+PB的值最小,接着利用待定系数法求出直线A′B的解析式,然后计算函数值为0时的自变量的值可得P点坐标.
解答 解:(1)把A(1,4)代入y=$\frac{m}{x}$得m=1×4=4,
所以反比例函数解析式为y=$\frac{4}{x}$;
(2)存在.
把B(4,n)代入y=$\frac{4}{x}$得4n=4,解得n=1,
所以B(4,1),
作点A关于x轴的对称点A′,如图,则A′(1,-4),连结A′B交x轴于P,则PA=PA′,
所以PA+PB=PA′+PB=A′B,
所以此时PA+PB的值最小,
设直线A′B的解析式为y=kx+b,
把A′(1,-4),B(4,1)代入得$\left\{\begin{array}{l}{k+b=-4}\\{4k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{b=-\frac{17}{3}}\end{array}\right.$,
所以直线A′B的解析式为y=$\frac{5}{3}$x-$\frac{17}{3}$,
当y=0时,$\frac{5}{3}$x-$\frac{17}{3}$=0,解得x=$\frac{17}{5}$,
所以P点坐标为($\frac{17}{5}$,0).
点评 本题考查了用待定系数法求反比例函数的解析式:先设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);再把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;接着解方程,求出待定系数;然后写出解析式.也考查了反比例函数的性质.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
| A. | x<$\frac{b}{a}$ | B. | x>$\frac{b}{a}$ | C. | x<-$\frac{b}{a}$ | D. | x>-$\frac{b}{a}$ |
 问题提出:“任意给定一个矩形A,是否存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一?”
问题提出:“任意给定一个矩形A,是否存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一?”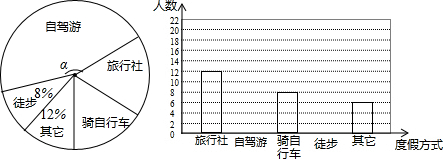
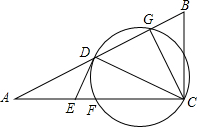 如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.
如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.