题目内容
9. 问题提出:“任意给定一个矩形A,是否存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一?”
问题提出:“任意给定一个矩形A,是否存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一?”为解决上面的问题,我们先来研究几种简单的情况:
(1)已知矩形A的边长分别为12和1,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一?
解:设所求矩形B的两边长分别是x和y,由题意得
$\left\{\begin{array}{l}{x+y=\frac{13}{3}}\\{xy=4}\end{array}\right.$,消去y化简得3x2-13x+12=0
∵△=169-144>0,
∴x1=$\frac{4}{3}$,x2=3,
∴已知矩形A的边长分别为12和1时,存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一.
(2)如果已知矩形A的边长分别为6和2,请依照上面的方法研究:是否存在满足要求的矩形B?
问题解决:如果已知矩形A的边长分别为m和n,请你研究,当m和n满足什么条件时,矩形B存在?
应用提升:如果在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象,其中x和y分别表示矩形B的两边长,请你结合刚才的研究,回答下面的问题:(直接写出结果即可,不需说明理由).
①该图象所表示矩形A的两边长各为多少?
②该图象所表示矩形B的两边长各为多少?
分析 (1)利用求根公式解方程即可;
(2)与(1)类似求解;
问题解决:依照(1)、(2)的解法,设所求矩形B的两边长分别是x和y,由题意得方程组$\left\{\begin{array}{l}{x+y=\frac{m+n}{3}}\\{xy=\frac{mn}{3}}\end{array}\right.$,消去y化简得3x2-(m+n)x+mn=0,然后根据判别式的意义求解;
应用提升:①利用函数图象和待定系数法得到一次函数和反比例函数解析式,则由$\left\{\begin{array}{l}{x+y=5.5}\\{xy=7.5}\end{array}\right.$,利用问题解决中的结论设矩形A的边长分别为m和n,则$\frac{m+n}{3}$=5.5,$\frac{mn}{3}$=7.5,然后求出m和n即可得到该图象所表示矩形A的两边长;
②对于①中的方程组消去y化简得x2-5.5x+7.5=0,人家利用求根公式解方程即可得到该图象所表示矩形B的两边长.
解答 解:(1)x=$\frac{13±5}{2×3}$,
所以x1=$\frac{4}{3}$,x2=3;
故答案为$\frac{4}{3}$,3;
(2)设所求矩形B的两边长分别是x和y,由题意得
$\left\{\begin{array}{l}{x+y=\frac{8}{3}}\\{xy=4}\end{array}\right.$,消去y化简得3x2-8x+12=0,
∵△=64-144<0,
∴方程3x2-8x+12=0没有实数解,
∴已知矩形A的边长分别为6和2时,不存在另一矩形B,它的周长和面积分别是已知矩形周长和面积的三分之一;
问题解决:设所求矩形B的两边长分别是x和y,由题意得
$\left\{\begin{array}{l}{x+y=\frac{m+n}{3}}\\{xy=\frac{mn}{3}}\end{array}\right.$,消去y化简得3x2-(m+n)x+mn=0,
∵△=(m+n)2-12mn=m2+n2-10mn,
当m2+n2≥10mn时,△≥0,方程有实数解,
∴当m和n满足m2+n2≥10mn时,矩形B存在;
应用提升:①一次函数解析式为y=-x+5.5,反比例函数解析式为y=$\frac{5×1.5}{x}$,
∴$\left\{\begin{array}{l}{x+y=5.5}\\{xy=7.5}\end{array}\right.$,
设矩形A的边长分别为m和n,则$\frac{m+n}{3}$=5.5,$\frac{mn}{3}$=7.5,解得m=15,n=1.5,即
∴该图象所表示矩形A的两边长分别为15和1.5;
②方程组消去y化简得x2-5.5x+7.5=0,
∵△=5.52-4×7.5>0,
∴x1=2.5,x2=3;
∴该图象所表示矩形B的两边长分别为2.5和3.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查一元二次方程得应用.解决本题的关键是方程思想的运用.

 如图,数轴上点A表示的数可能是 ( )
如图,数轴上点A表示的数可能是 ( )| A. | $\sqrt{3}$ | B. | -2.3 | C. | -$\sqrt{3}$ | D. | -2 |
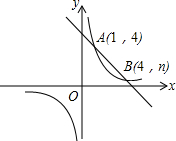 如图,直线AB与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,直线AB与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
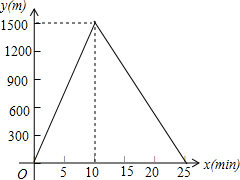 小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.