题目内容
2．
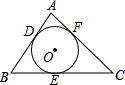如图所示，⊙O分别切△ABC的三边AB、BC、CA于点D、E、F，若BC=10，AC=11，AB=8，求AF、BD、CE的长．
分析 利用切线长定理列方程求解即可．
解答 解：∵⊙O分别切△ABC的三边AB、BC、CA于点D、E、F，
∴AD=AF、BD=BE、FC=EC．
设AF=AD=x，则BD=BE=8-x，FC=EC=11-x．
∵BC=10，
∴8-x+11-x=10．
解得；x=4.5．
∴AF=4.5．
∴BD=8-4.5=3.5，CE=11-x=11-4.5=6.5．
点评 本题主要考查的是三角形的内切圆与内心，利用切线长定理列出关于x的方程是解题的关键．
练习册系列答案
相关题目
12．有一旅客携带了35千克行李从天河机场去北京，按规定旅客最多可免费携带20千克行李，超过部分每千克按飞机票价的1.5%购买行李票．现该旅客买了225元行李票，则他的飞机票价为（ ）
| A． | 800元 | B． | 1000元 | C． | 1200元 | D． | 1600元 |
13．在平面直角坐标系中．已知点A（4，0）点B（0，3）．点P在x轴上，且△ABP为等腰三角形，则P点有（ ）个．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
已知：如图，CD是Rt△ABC的斜边AB上的高，用余弦、正切的定义证明：
已知函数y=-（x-m）2+n．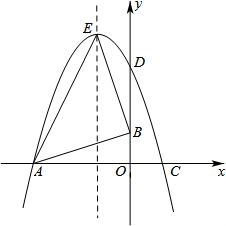
如图，在直角坐标系中，O是坐标原点，已知△OAB的顶点A（-6，0），B（0，2），将△OAB绕点O按顺时针旋转90°，得到△ODC．
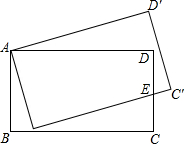如图所示，将矩形ABCD旋转到AB′C′D′位置，使边BC恰好经过边CD的中点E．若AB=8，C′E=2，则四边形AB′ED的面积是70．
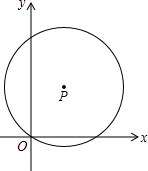如图，在平面直角坐标系xOy中，点P（a，b）在第一象限．以P为圆心的圆经过原点，与y轴的另一个交点为A．点Q是线段OA上的点（不与O，A重合），过点Q作PQ的垂线交⊙P于点B（m，n），其中m≥0．