题目内容
10.按照一定顺序排列的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n位的数称为第n项,记为an.一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…,为等比数列,其中a1=1,公比为q=3.
(1)等比数列3,6,12,…,的第6项是96.
(2)如果一个数列a1,a2,a3,a4,…,是等比数列,且公比为q.根据定义可得到:$\frac{{a}_{2}}{{a}_{1}}$=q,$\frac{{a}_{3}}{{a}_{2}}$=q,$\frac{{a}_{4}}{{a}_{3}}$=q,…,$\frac{{a}_{n}}{{a}_{n-1}}$=q.所以a2=a1•q,a3=a2•q=(a1•q)•q=a1•q2,a4=a3•q=(a1•q2)•q=a1•q3,…,由此可得:an=a1•qn-1(用a1和q的代数式表示).
(3)若用Sn表示等比数列a1,a2,a3,a4,…,an,中前n项和.证明分两种情况:当q=1时,a2=a1,a3=a1,a4=a1,…,∴Sn=a1+a2+a3+…+an=na1.
①根据q=1的证明方法,证明:当q≠1时,等比数列前n项和Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$成立.
②求(1)中等比数列S6的值.
分析 (1)根据等比数列的定义先确定公比q=2,继而可得;
(2)根据题意得出每一项等于首项乘以公比的序数减1次方,据此可得;
(3)①由题意得Sn=a1+a2+a3+…+an=a1+a1•q+a1•q2+…+a1•qn-1,则qSn=a1•q+a1•q2+…+a1•qn-1+a1•qn,两式相减整理可得答案;②将a1=3、q=2、n=6代入求解可得.
解答 解:(1)∵该等比数列的公比q=6÷3=2,
∴数列第4项为12×2=24,第5项为24×2=48,第6项为48×2=96,
故答案为:96;
(2)∵a2=a1•q,a3=a2•q=(a1•q)•q=a1•q2,a4=a3•q=(a1•q2)•q=a1•q3,…,
∴an=a1•qn-1,
故答案为:a1•qn-1;
(3)①当q≠1时,
∵a2=a1•q,a3=a1•q2,a4=a1•q3,…,an=a1•qn-1,
∴Sn=a1+a2+a3+…+an=a1+a1•q+a1•q2+…+a1•qn-1 ①,
则qSn=a1•q+a1•q2+…+a1•qn-1+a1•qn ②,
①-②,得:(1-q)Sn=a1-a1•qn=a1(1-qn),
∵q≠1,
∴q-1≠0,
则Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$;
②∵等比数列3,6,12,…,的首项a1=3,公比q=2,
∴S6=$\frac{3×(1-{2}^{6})}{1-2}$=189.
点评 本题主要考查数字的变化类,阅读材料,理解等比数列的定义及数列求和的方法是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
19.计算$\frac{2}{3}$×(-$\frac{9}{4}$)的结果等于( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
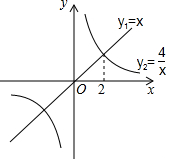 函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.
函数y1=x与y2=$\frac{4}{x}$的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是①③.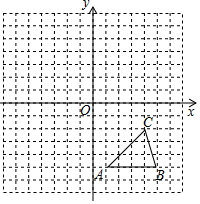 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2). 已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.
已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.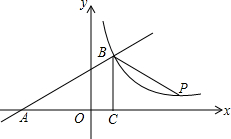 如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点.
如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),点P(3n-4,1)是反比例函数图象上的一点. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.
如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.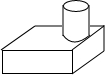 由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )
由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )