题目内容
14.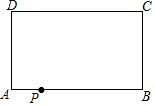 如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.
如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.(1)在图(1)中利用无刻度的直尺和圆规作出直线l.(保留作图痕迹,不写作法和理由)
(2)若PD′⊥PD,①求线段AP的长度;②求sin∠QD′D.
分析 (1)根据题意作出图形即可;
(2)由(1)知,PD=PD′,根据余角的性质得到∠ADP=∠BPD′,根据全等三角形的性质得到AD=PB=4,得到AP=2;根据勾股定理得到PD=$\sqrt{A{D}^{2}+A{P}^{2}}$=2$\sqrt{5}$,CD′=$\sqrt{DD{′}^{2}-C{D}^{2}}$=2,根据三角函数的定义即可得到结论.
解答  解:(1)连接PD,以P为圆心,PD为半径画弧交BC于D′,
解:(1)连接PD,以P为圆心,PD为半径画弧交BC于D′,
过P作DD′的垂线交CD于Q,
则直线PQ即为所求;
(2)由(1)知,PD=PD′,
∵PD′⊥PD,
∴∠DPD′=90°,
∵∠A=90°,
∴∠ADP+∠APD=∠APD+∠BPD′=90°,
∴∠ADP=∠BPD′,
在△ADP与△BPD′中,$\left\{\begin{array}{l}{∠A=∠B=90°}\\{∠ADP=∠BPD′}\\{PD=PD′}\end{array}\right.$,
∴△ADP≌△BPD′,
∴AD=PB=4,
∵PB=AB-AP=6-AP=4,
∴AP=2;
∴PD=$\sqrt{A{D}^{2}+A{P}^{2}}$=2$\sqrt{5}$,
∵PD=PD′,PD⊥PD′,
∵DD′=$\sqrt{2}$PD=2$\sqrt{10}$,
∴CD′=$\sqrt{DD{′}^{2}-C{D}^{2}}$=2,
∴sin∠QD′D=sin∠QDD′=$\frac{CD′}{DD′}$=$\frac{2}{2\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
点评 本题考查了作图-轴对称变换,矩形的性质,折叠的性质,全等三角形的判定和性质,等腰直角三角形的性质,正确的作出图形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某微生物的直径为0.000 005 035m,用科学记数法表示该数为( )
| A. | 5.035×10-6 | B. | 50.35×10-5 | C. | 5.035×106 | D. | 5.035×10-5 |
9.在综合实践话动课上,老师组织大家利用两块大小相同的含30°角的三角板进行拼接组合(不重叠)的探索活动,在讨论所组合而成的图形过程中,所得下列四个结论中错误的是( )
| A. | 当两块三角板的斜边完全拼接在一起时,所拼成的图形一定是轴对称图形 | |
| B. | 当两块三角板的对应直角边完全拼接在一起时,所拼成的图形可能是等边三角形 | |
| C. | 当两块三角板可以通过平移后重合时,所拼成的图形不可能是轴对称图形 | |
| D. | 当两块三角板只有直角顶点拼接在一起时,所拼成的图形不可能是中心对称图形 |
19.计算$\frac{2}{3}$×(-$\frac{9}{4}$)的结果等于( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
6.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.据统计,“五一”小长假期间,大连市共接待海内外游客825400余人次,数825100用科学记数法表示为( )
| A. | 8251×102 | B. | 825.1×103 | C. | 82.51×104 | D. | 8.251×105 |
4.在用电水壶加热水的过程中,电水壶里的水温随通电时间的长短而变化,这个问题中的自变量是( )
| A. | 通电的强弱 | B. | 通电的时间 | C. | 水的温度 | D. | 电水壶 |
 已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.
已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.
如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为45°.