题目内容
8.定义:对于任意一个不为1的有理数a,把$\frac{1}{1-a}$称为a的差倒数,如2的差倒数为$\frac{1}{1-2}=-1$,-1的差倒数为$\frac{1}{1-(-1)}$=$\frac{1}{2}$.记${a_1}=\frac{1}{2}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2=2;a2015=2.分析 首先根据a1=$\frac{1}{2}$,可得a2=$\frac{1}{1{-a}_{1}}=\frac{1}{1-\frac{1}{2}}=2$,a3=$\frac{1}{1{-a}_{2}}=\frac{1}{1-2}=-1$,${a}_{4}=\frac{1}{1{-a}_{3}}=\frac{1}{1-(-1)}=\frac{1}{2}$,…,所以这列数是$\frac{1}{2}$、2、-1、$\frac{1}{2}$、2、-1、…,每3个数是一个循环;然后用2015除以3,求出一共有多少个循环,还剩下几个数,进而判断出a2015的值是多少即可.
解答 解:因为a1=$\frac{1}{2}$,
所以a2=$\frac{1}{1{-a}_{1}}=\frac{1}{1-\frac{1}{2}}=2$,
a3=$\frac{1}{1{-a}_{2}}=\frac{1}{1-2}=-1$,
${a}_{4}=\frac{1}{1{-a}_{3}}=\frac{1}{1-(-1)}=\frac{1}{2}$,
…,
所以这列数是$\frac{1}{2}$、2、-1、$\frac{1}{2}$、2、-1,…,每3个数是一个循环,
因为2015÷3=671…2,
所以a2015=2.
故答案为:2、2.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数是$\frac{1}{2}$、2、-1、$\frac{1}{2}$、2、-1,…,每3个数是一个循环.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
19.点P是直线l外一点,点A、B、C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( )
| A. | 6 | B. | 8 | C. | 不大于6的数 | D. | 小于6的数 |
19.某商品原价168元,经过连续两次降价后的售价为128元,设平均每次降价的百分数为x,则下面所列方程中正确的是( )
| A. | 168(1+x)2=128 | B. | 168(1-x)2=128 | C. | 168(1-2x)2=128 | D. | 168(1-x2)=128 |
16.2015年是第23个“世界水日”,为鼓励居民节约用水,某市规定如下用水收费标准:每户每月的用水量不超过6m3时,水费按a元/立方米收费;超过时,不超过6m3的部分仍按a元/立方米收费,超过的部分按c元/立方米(c>a)收费,已知该市小明家今年3月份和4月份的用水量、水费如表所示:
(1)求a,c的值;
(2)设某户1个月的用水量为x(m3),应交水费y(元)
①分别写出用水量不超过6m3和超过6m3时,y与x之间的函数关系式;
②已知一户5月份的用水量为8m3,求该户5月份的水费.
| 月份 | 用水量/m3 | 水费/元 |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(2)设某户1个月的用水量为x(m3),应交水费y(元)
①分别写出用水量不超过6m3和超过6m3时,y与x之间的函数关系式;
②已知一户5月份的用水量为8m3,求该户5月份的水费.
 如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,则直线EF与BC的位置关系是平行.
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,则直线EF与BC的位置关系是平行.
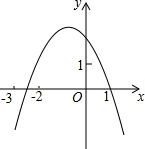 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( ) 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)