题目内容
5.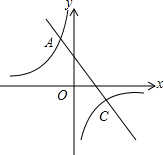 如图,点C是反比例函数y=$\frac{k}{x}$(k<0)图象上的一点,点C的坐标为(4,k+3).
如图,点C是反比例函数y=$\frac{k}{x}$(k<0)图象上的一点,点C的坐标为(4,k+3).(1)求反比例函数解析式;
(2)若一次函数y=ax+3的图象经过点C,交双曲线的另一支于点A,求点A的坐标;
(3)在x轴上是否存在点P,使得△PAC的面积为10?如果存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)把C(4,k+3)代入y=$\frac{k}{x}$解方程即可得到结论;
(2)把C(4,-1)代入y=ax+3得到y=-x+3,解方程组即可得到结论;
(3)根据△PAC的面积为10,列方程$\frac{1}{2}$|x-3|×4+$\frac{1}{2}$|x-3|×1=10,即可得到结论.
解答 解:(1)把C(4,k+3)代入y=$\frac{k}{x}$得k+3=$\frac{k}{4}$,解得:k=-4,
∴反比例函数解析式为:y=-$\frac{4}{x}$;
(2)把C(4,-1)代入y=ax+3得-1=4a+3,解得a=-1,
∴y=-x+3,
则$\left\{\begin{array}{l}{y=-\frac{4}{x}}\\{y=-x+3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$,
∴A(-1,4);
(3)存在,设P(x,0),直线AC与x轴的交点为M,
∴M(3,0),
∵△PAC的面积为10,
∴$\frac{1}{2}$|x-3|×4+$\frac{1}{2}$|x-3|×1=10,
∴x=-1,或x=7,
∴P(-1,0),(7,0).
故存在点P,使得△PAC的面积为10.
点评 本题考查了反比例函数和一次函数图象的交点问题,反比例函数系数的几何意义,反比例函数图象上点的坐标特征,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,三角形的面积是$\frac{1}{2}$|k|.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
15.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是0.25;(精确到0.01)
(2)估算袋中白球的个数.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
| 摸到黑球的频率$\frac{m}{n}$ | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 | 0.251 |
(2)估算袋中白球的个数.
20.已知y是x的一次函数,其部分对应值如下表:
(1)求这个一次函数的表达式,并补全表格;
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
| x | -3 | 0 | 3 | 5 |
| y | -4 | 2 | 8 | 12 |
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
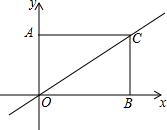 有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.
有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.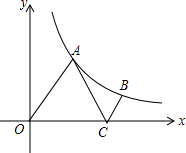 如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.
如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.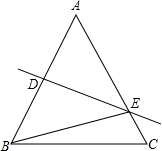 如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.
如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.