题目内容
1. 如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.
如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.(1)在上述移动过程中,对于四边形ABCD的说法不正确的是B
A.面积保持不变 B.只有一个时刻为菱形
C.只有一个时刻为矩形 D.周长改变
(2)在上述移动过程中,如图2,若将△ABD沿着BD折叠得到△A′BD(点A′与点C不重合),A′B交CD于点D.
①试问A′C与BD平行吗?请说明理由;
②若以A′、D、B、C为顶点的四边形是矩形,且对角线的夹角为60°,求AD的长.
分析 (1)根据平移的性质进行判断即可;
(2)①根据对折的性质得出对应边和角相等,再根据平行线的判定解答即可;
②根据矩形的性质和等边三角形的性质进行分析解答.
解答 解:(1)因为平移,AB保持不变,且AB与CD间的距离不变,所以四边形ABCD的面积不变,故A正确;
当AD⊥CD时,四边形ABCD可以是矩形,故C正确;
因为AD的长度有变化,所以四边形ABCD的周长改变,故D正确;
故选B.
(2)①A'C∥BD.理由如下:
如图2,
由?ABEF可得,AB=CD,AB∥CD,
又根据对折可知AB=A'B,∠3=∠2,
∴A'B=CD,∠1=∠3,
∴OD=OB.
∴OA'=OC,
∴∠4=∠5.
∵∠BOD=∠A'OC,
∴∠4+∠5=∠1+∠3,
即∠1=∠4,
∴A'C∥BD.
②如图3,
由①知CD=AB=2,∠1=∠2,∠A=∠3.
当四边形A'DBC矩形时,有∠DBC=90°,OA'=OD=OB=OC=1.
当∠A'OD=60°,则∠DOB=120°,
∴∠1=30°.
∴∠2=30°,∠A=∠3=60°.
∴∠ADB=90°.
∴在Rt△ADB中,$AD=\frac{1}{2}AB=1$.
当∠DOB=60°(如图4),
则△ODB为正三角形,
∴∠2=∠1=60°,∠A=∠3=30°,BD=OD=1.
∴∠ADB=90°.
∴在Rt△ADB中,$tan∠2=\frac{AD}{BD}$,
∴$AD=BD•tan∠2=1•tan60°=\sqrt{3}$.
综上可得,AD的长为1或$\sqrt{3}$.
点评 本题考查了几何变换,解题的关键是根据平移和对折的性质分析,同时注意矩形和等边三角形的有关知识.

练习册系列答案
相关题目
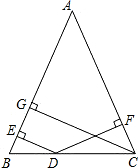 如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.
如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.DE,DF,CG的长之间存在着怎样的等量关系?并加以证明. 如图,∠B=46°,∠D=42°,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P=45°.
如图,∠B=46°,∠D=42°,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P=45°.